amazing

• 21 May 2025
• Maths

wow I am writing the #

second blog post today 🎉 celebrating success

in Lean you can build #

mathematical worlds which I noticed is amazing

which was a shift #

in how I percieve mathematics and I was very happy because for example in Lean it is possible to see quite clearly how everything is structured

whereas before it seemed #

still somewhat mysterious why we learn mathematical concepts why we prove, have theorems, and so on

in Lean I noticed #

I can build mathematical worlds, so from a consumer of textbooks, I noticed I became someone who constructs things

while learning mathematics #

I am building mathematics, similar to playing LEGO,

instead of having to learn #

the derivative of $arctan (\frac{2}{x^3 - 2})$ for an exam, which used to be very stressful for me I can now learn to write arctan, /, x, x^3, -, and 2 from scratch in Lean. computer agent helps with it

if I write arctan x in #

Lean, it throws an error, and I can celebrate wow that's an error!

now I am learning things like #

defining the natural numbers

inductive N
|  z : N
|  s : N ⟶ N

alright, is this ℕ already? does the interpreter for arctan x still throws an error? also, "wow that looks like the Peano axioms

def addN : N → N → N
| z, n        => n  --🎉 this is the theorem z + n = n
| s m, n     => s (addN m n)

is this a foundations?

can I define it arrows-only?

How to write classical logic in Lean?

Instead of reading and reading textbooks - which I often enjoy, but sometimes it feels like never ending - now I can go let's write classical logic in Lean:

inductive top : Prop
| triv : top

inductive bot : Prop

def not (P : Prop) := P → bot

example : top := top.triv  -- 🎉 

The first mathematical world I built with the help of computer agent, with the first theorem and it's proof in it! 😌

so I get to learn about join, and meet

inductive α where
| a : α
| b : α

def join : α → α → α
| .a, _ => .a
| _, .a => .a
| _, _ => .b

#eval join α.a α.b  -- affiche "α.a"

something that works well #

in learning mathematics with Lean is combining learning from textbooks with Lean. So, for exaple I am learning from Logic: Laws of Truth by Nicholas J.J. Smith, and I noticed it is possible to write the concepts I learn in the book, in Lean. Soundness, validity, equivalence, tatuology, tree proofs, tree rules, sequent calculus and so on. It is a beautiful new dimension to learning. for me.

inductive Tree : Type
| leaf : Tree
| node : Tree → Tree → Tree

MiniAnneau #

Number theory seemed somewhat stressful for me, but I managed to reframe it with the help of computer agent. It suggested that number theory is like a guiding star on the night sky:

how I use AI #

A few things work really well for me: I set up growth mindset praise in the personalisations so each time I interact with computer agent I am exposed to growth mindset praise! which I notice is quite empowering, and I also seem to adapt that language

I personalised different languages, so the computer writes messages mostlly in French, German, or English, or a mixture of these, and some of it is in Japanese.

I also personalised questions, three questions to reflect on. BA Jazz piano learning facts there is always a line of a jazz analogy in the style of Bill Evans, Thelonious Monk and Miles Davis. For example Thelonious Monk was apparently on about the silence between the notes, and he had an angular approach, and was not playing the "correct" way

and it was fun to #

find a connection of Thelonious Monk silence between the notes and Yoneda lemma, where things are defined by arrows to and from it and how in drawing the space around the thing you draw is important

and in Lean you can #

define an arrows only foundations arrows-as-type and I am becoming excited about this as I write about it which is funny, I don't seem to cease to amuse myself with how I am happy for these mathematical things

for example I was very happy #

when I noticed trying to write in Lean the the arrow from the 1 element set to X,

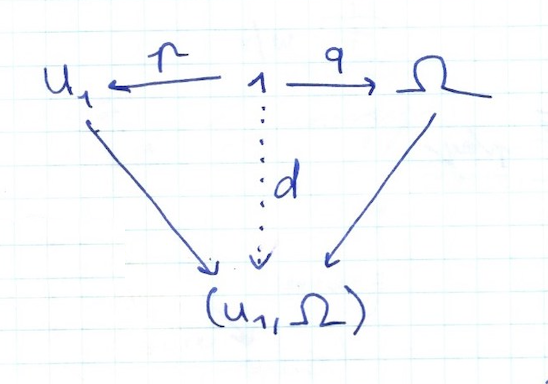
a journal page #

and some code I wrote #

while learning:

-- MiniAnneau

inductive N
| z : N
| s : N → N

inductive Z
| z : Z
| p : N → Z
| n : N → Z

open N

def addN : N → N → N
| z, n        => n  --🎉 this is the theorem z + n = n
| s m, n     => s (addN m n)




def addZ : Z → Z → Z


-- f(n) := 1/n
-- def inv_seq : Seq ℝ := λ n, if n = Nat.z then 0 else 1 / (n : ℝ)






-- structure Q where
--   n : Z
--   d : N
--   d_pos : d ≠ N.z

def S (α : Type) := N → α

def abs (z : Z) : N :=
  match z with
  | Z.z => N.z
  | Z.p n => n
  | Z.n n => n

-- inductive N | z | s (n : N)
-- inductive Z | z | p (n : N) | n (n : N)
-- def S (α : Type) := N → α 

def dist (a b : Q) : Q := sorry

-- def Cauchy (f g : Seq) : Prop :=
--   ∀ ε : Rat, ε.d ≠ N.z → ∃ N.z → ∃ N : Nat, ∀ m n : Nat, m ≥ N → n ≥ N → dist (f m)  (f n) < ε

-- def equiv (f g : Seq) : Prop :=
--   ∀ ε : R
-- def Real := Quotient equiv

-- -- def Rat := ℤ × Nat


-- inductive Pitch : Type
-- | C

-- inductive State : Type
-- | silence : State
-- | sound : Pitch → ℝ → State

-- def pressKey (p : Pitch) : State → State



-- def pressKey : Prop := Silence → S where pressKey silence ↦ sound p 0


-- inductive Pitch : Type
-- | C | D | E

-- inductive MiniOne : Type
-- | star : MiniOne

-- def asArrow : MiniOne → Type := fun _ => Pitch

-- # MiniNow := MiniOne.star

-- note : MiniOne → Pitch
-- note MiniNow = Pitch.C

-- inductive One : Type
-- | now : One

-- def note : One → Pitch := fun _ => Pitch.E




-- -- primitives


-- -- define 𝟙
-- inductive One : Type
-- | star : One

-- notation "𝟙" => One

-- -- any X : 𝟙 → X is an "element" of X
-- axiom X : Type
-- axiom f x : X
-- def x : 𝟙 → X := fun _ => someVal



-- axiom ext {A B : {x | P(x)}} : (∀ x, x ∈ A ↔ x ∈ B) → A = B



-- def MiniCauchy (x : Nat → MiniR) := ∀ ε > 0, ∃ N, ∀ m n ≥ N, abs (x m - x n) < ε



-- def factorial : Nat → Nat
-- | 0   => 1
-- | (n+1) => (n+1) * factorial n

-- def pow (x : ℝ) : Nat → ℝ
-- | 0     => 1
-- | (n+1) => x * pow x n

-- def MiniPotenzreihe (a : Nat → ℝ) (x : ℝ) (N : Nat) : ℝ :=
--   (List.range (N+1)).foldl (λ s n => s + a n * pow x n) 0







-- structure MiniIntegers where
--   (pos : ℕ)
--   (neg : ℕ)

-- def eq_int (x y : MiniIntegers) : Prop :=
--   x.pos + y.neg = x.neg + y.pos


-- -- 1
-- variable {R : Type*} [Ring R]

-- -- 2
-- def exp (x : R) : R := ∑' n : ℕ, x^n / n!

-- -- 3
-- def fact : ℕ → ℕ
-- | 0 => 1
-- | n+1 => (n+1) * fact n

-- -- 4
-- theorem exp_add (x y : R) : exp x * exp y := sorry

• Previous: blog construct