Square partitions

• 02 March 2024
• Data Science,
• Learning,
• Writing,
• Python,
• Music,
• Maths

Rephrasing of a combinatorial problem #

Hányféleképpen lehet egy n^2 négyzetszámot k db, 0 <= x <= n, x számjegy összegével kifejezni? Pl 4 kifejezhető |{"1+1+2", "1+2+1", "2+1+1", "2+2+0", "2+0+2", "0+2+2"}|=6 féleképpen, ha n=2, és k=3

How many ways can n^2 be written as a sum of k non-negative integers d <= n? For example, we can write 4 |{"1+1+2", "1+2+1", "2+1+1", "2+2+0", "2+0+2", "0+2+2"}|=6 ways, if n=2, and k=3.

A = {kavics | kavics ∈ N, 0 =< kavics =< n} halmazból választhatunk kavicsokat, és B = {ág | ág ∈ N} halmazból ágakat, úgy, hogy az összes kiválasztott kavics összege n^2 legyen, és egy ág mellé maximum n kavics rakható.

Kellett nekem matematika tanulásba kezdeni! 😉

$C(n, k) * \sum_{i=0}^{min(k, n)} C(n, i) * C(n - i, k - i)$

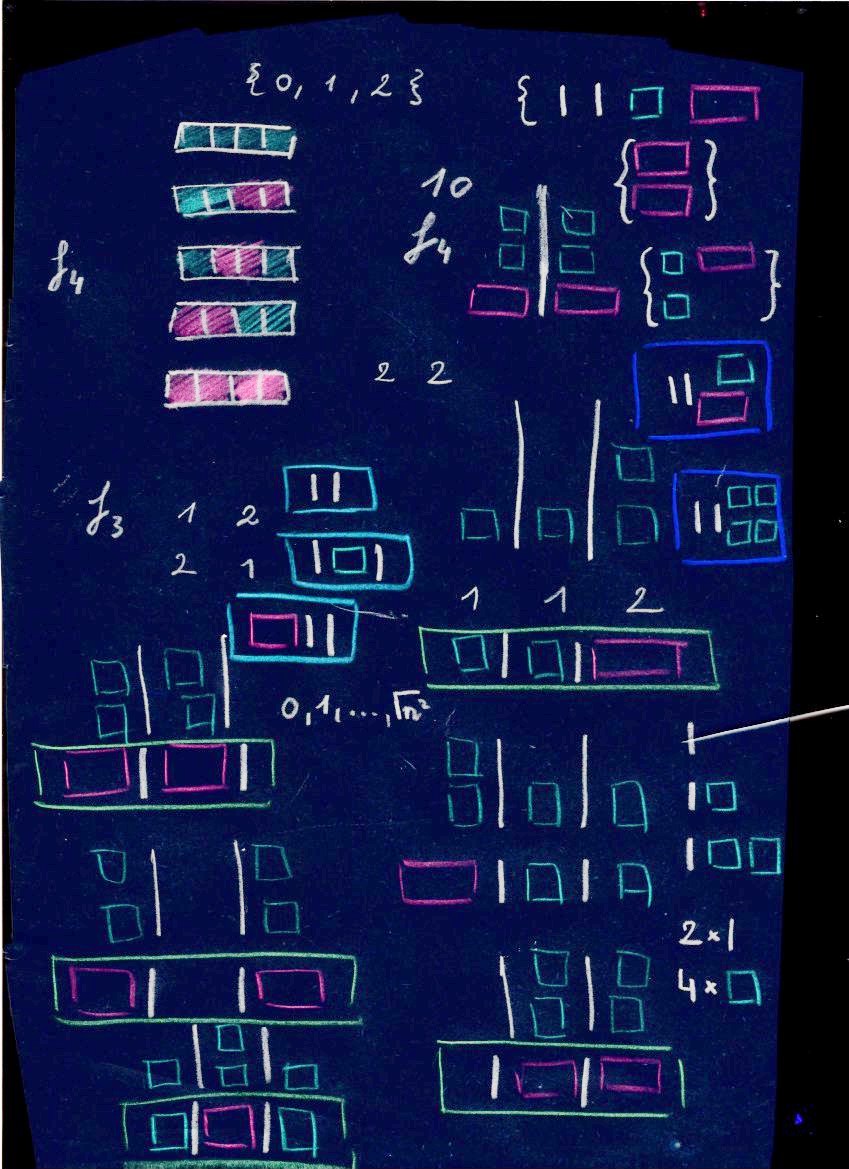
I received this cool paper in collaboration:

• Notes on partitions and their generating functions

• Previous: The sunshiny day, we are the world
• Next: Physics tutorial