Data Science Wizardry Blog by Attila Vajda

Mozart, chants, sunlight and rubber duck

Wuthering Heights #

Reading. Yesterday I learnt about the importance of improving working memory, and that reading fiction is a way to do it. Now I have the idea to collaborate with computer agent on summarizing chapters, and combining this activity with the TWR technique. Writing, I suppose, is also beneficial for the nervous system.

A morning photo of a glass of water, with low solar angle sunglight illuminating the glass, and water, creating awesome elongated shadows and mathematical patterns. Shadows of a tree dance on the table, and the colors mix.

Binomial meanderings #

What are binomial expressions? How does the binomial distribution connect to binomial coefficients?

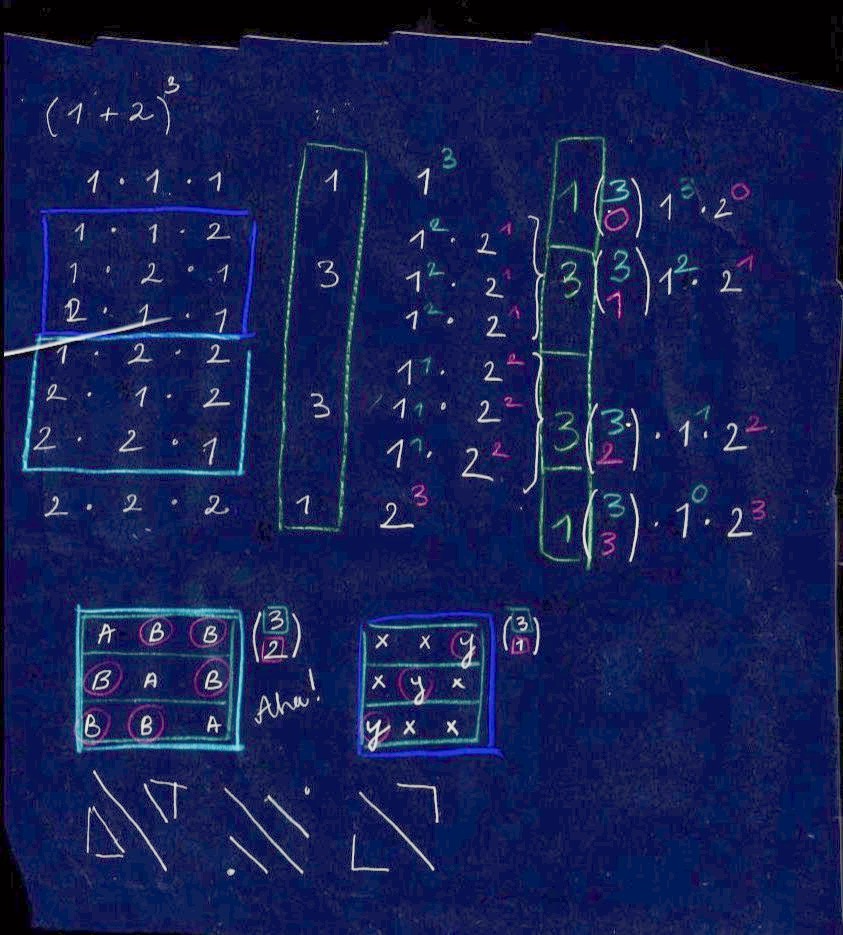
Binomial, polynomial,

How does a+b connect to statistics, and to the art of counting?

2xy captures both combinations xy and yx, as combinations ignore the sequence of elements

Why do we select x, and y?

(x + y)^1

1, 1

(x + y)(x + y)

1, 2, 1

x^2 * xy * yx * y^2

(10 + 7)(10 + 7)

$(10 * 10) + (10 * 7) + (7*10) + (7 * 7)$

(10 + 7)(10 + 7)(10 + 7)

$(10*10*10)+(10*10*7)+(10*7*10)+(7*10*10)+(10*7*7)+(7*10*7)+(7*7*10)+(7*7*7)$

$3 \choose 1$

(x+y)^2 reflects all possible combinations of picking x and y Nice, does it?

" For example, in the expansion of $(a+b)^n$, the term $a^k⋅b^{n−k}$ represents the probability of obtaining $k$ successes and $(n−k)$ failures in $n$ trials. ""

What worked is plugging in values, trying the formulas with small numbers. Trying to read the notation as if it was language, as the authors do in the "Proofs the Count":

Notation of combinatorial rephrasing of n!, and its description

Multiplying with $n \choose k$ can be read as we read words, but I don't yet clearly see how. We can arrange books on a shelf n! ways, and the number of ways will be equal to this, when we select nCk books, arrange them in k! ways, and then arrange the rest of the books (n-k)! ways. I think the focus is on the number of ways to arrange, not on actual arranging.

How the binomial coefficient connects to binomial distribution, and expansion, notes

Revisiting the notes I took for including it in the blog seems to be beneficial, because it helps with intermittent learning. Now I need to explain what is it that I wrote two days ago, so it is awesome. I wondered, how binomial coefficient connects to nCk, elements, binomial distribution, and the Pascal's triangle. The epiphany occured after writing down the explicit expansion of terms, x*x*x, x*x*y ..., because I could see the same pattern of arranging elements like AB, and 01, and {sound, silence} in rhythm. We seem to multiply by nCk, to account for the repetition of selections.

Seeing the bell shape curve correspond to lines of Pascal's triangle was another epiphany. My mind wants to read nCk*something as English, but I don't yet see the meaning of "multiplying by the n-th row and k-th column of the triangle".

I also wondered what 2^n meant, and expanding the terms made it clear, that it was all the possible arrangements, or variations of {x, y} in n slots. This work is still often very frustrating, but using the many techniques of learning how to learn, and the multidimensional approach I experience a lot of success. I am often amazed, how a subject, to me inaccessible, became fun, playful, and engaging.

Using coloring pencils, mixed media, manipulatives, a multidimensional, playful approach, and being loose with the material definitely contributes to the delightful experience of exploring mathematics.

"I love it! ❤️" finally I am rereading my notes with open eyes.

Notes of binomial expansion, (nCk)(x^n)(y^k)

(nCk)*(x^n)*(y^k) this is what I was trying to understand. Wow, and now I see n-k is the power we raise x to.

Biscotti count times

Plugging in 1, 2, and 3 for (x+y)^n, and colorcoding what the terms mean in the expansion, and combination of elements.{: .caption}

How many task #

A task for finding many people are there in a group

This is a problem I struggle with.

February workspace, with journal, color pencils, soft ball, a pillow/mat for sitting, tshirt, advanced mathematics textbook, coffee cup and glass of water. My bare feet and toes. Sunlight, garden.