What is the chance of rolling 6 with a die?
What is the chance of rolling 6 with a die on s rolls? #
Struggling with combinatorics seems to be effective, so I am doing it.
An analogous problem is finding the chance of rolling exactly two sixes with 30 dice.
Practicing the "art of counting" mentally is a good cognitive exercise. I count in triangular numbers, primes, factorials, and Fibonacci numbers forwards and backwards, while noting the index of numbers in binary form, using my fingers!
1-((5**s)/(6**s))
I used my fingers and my two hands to find the different possible variations of choosing two from five elements, and taking their permutations. For a simpler form, I looked at choosing from 2 elements ['1','2'] The chance of choosing at least one '1' is the complementer of not choosing a '1'. If we have elements 'AB', then we can vary these elements in 4 ways: 'AA', 'AB', 'BA, 'BB'. The probability of not choosing 'A' is P(A)=1/4, so the probability of choosing at least one is $P(\overline{A})=1-(1/4)$. I also looked at analogous problems on Discord, and found some insight, so it is worth looking at other people's efforts at solving similar problems.

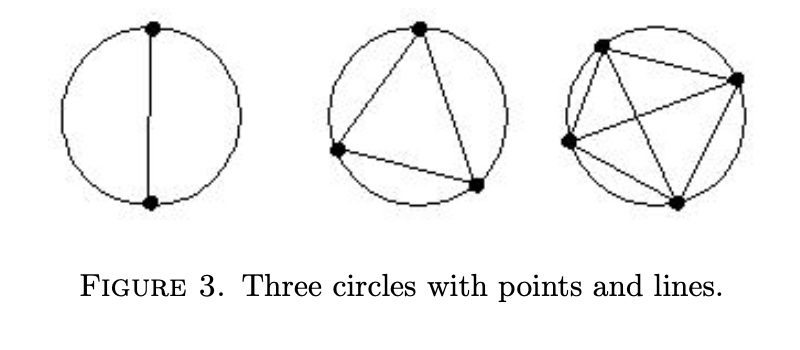
It is interesting, that combinations can be visualised with dots, and edges connecting them. I wondered if the enclosing spaces edges create have meaning, in terms of elements we observe.
- Previous: Chopin's Fantaisie Impromptu
- Next: Struggling