Statisztika, caffeine might be neuroprotective
How does the combination formula #
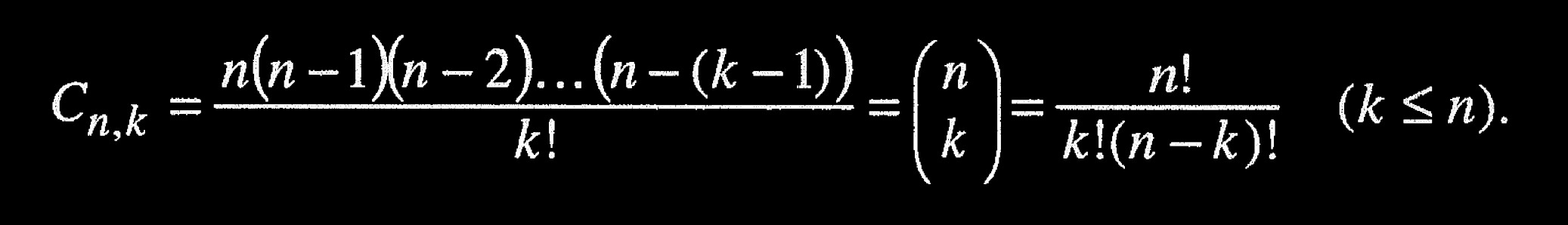
How $n!$ has $(n-k)!$, and what does $n(n-1)(n-2)...(n-(k-1))$ mean?

It is very interesting to make the connections of the abstract symbols, and of the concrete examples, patterns, but I certainly struggle with this. This seems to be very good exercise in learning to think algebraically. I also feel that "this is not something I can ever learn", and "it takes too long, I'm not good at it", but I already know that these are indications of learning taking place!
I can see that we are combining the components permutation, variation, combination, elements, number of elements, and number of choices.
What is the difference of 6C3, and $C_{6,3}^{3}$?
Why $C_{6,3}^{3}$ is $8C3$, in terms of patterns?

What is the difference between $C^i_{n,k}$ and $V^i_{n,k}$?
$V^i_{n,k}$ for "ab" could be $V^i_{2,2}$, $2*2$, $2^2$: ['aa','ab','ba','bb']
$C^i_{n,k}$ for "ab" could be $C^i_{2,2}$ ['aa','ab','bb']
I'm not sure how to write it more accurately in Python.
I don't know what the (2+2+1)!, (n+k+1)! in the numerator is in the repeating combinations example. Why do we add k and 1?
Why is $(𝑛−1)−(𝑘−1)=𝑛−𝑘$?
So cool! 🤓
- Previous: If you have ghosts
- Next: Chopin's Fantaisie Impromptu