I could relax my wrists, it's awesome!
I could relax my hands wrists, it's awesome! #
I tried to recreate the Feldenkrais method from what I read from the Norman Doidge book 'The Brain's Ways of Healing', and I found it difficult to relax my hands. It seemed easier to bend my wrist one way, and the other, with my forearm perpendicular to the floor, while listening to how the movement is produced. On one side of the forearm the muscles contract, while on the other side of it they relax. At one point I found that if my muscles were relaxed, changing the angle of my forearms with the floor, my hands would be tilted by gravity. This seemed like the ideal relaxation state, so I tried to compare it and translate it to other parts of my body. I don't know if this is the Feldenkrais method, or not, but I felt very peaceful, because I experienced the relaxation of my muscles. I tried to become aware of similar tension, relaxation patterns in other parts of my muscles. Part of the method is to reflect on changes in the entire body, and to become aware how one movement is connected to every other.
Shortcuts to 8!/4!4!, and 12!/6!6! #
Are there shortcuts, patterns to this calculation?
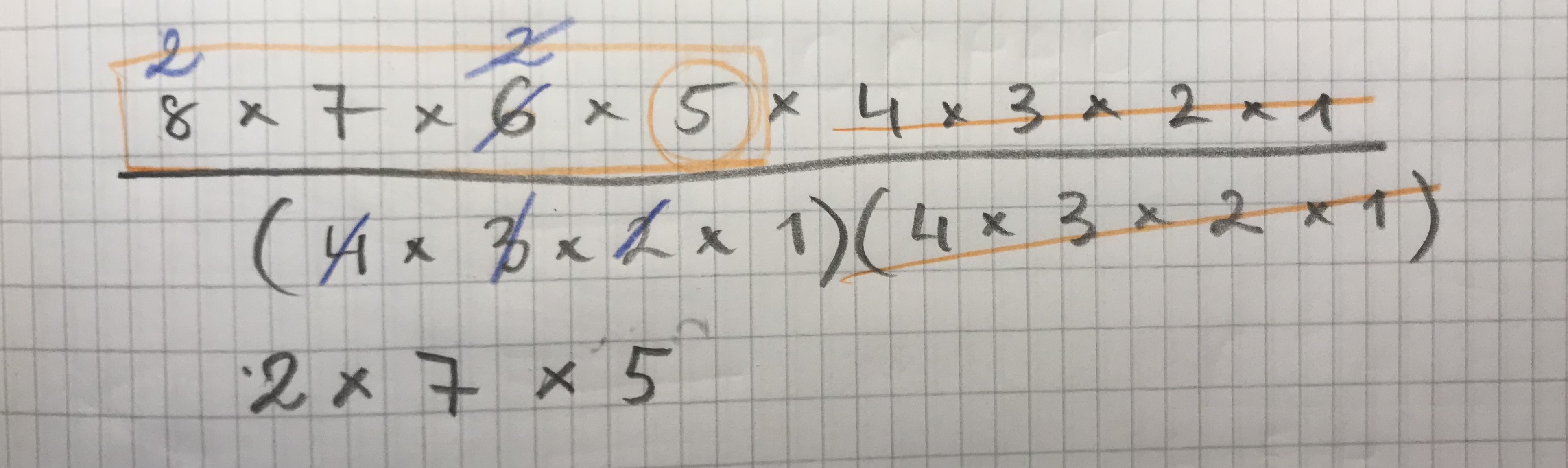
I am canceling out shared factors. 4!/2!2! = C_4,2
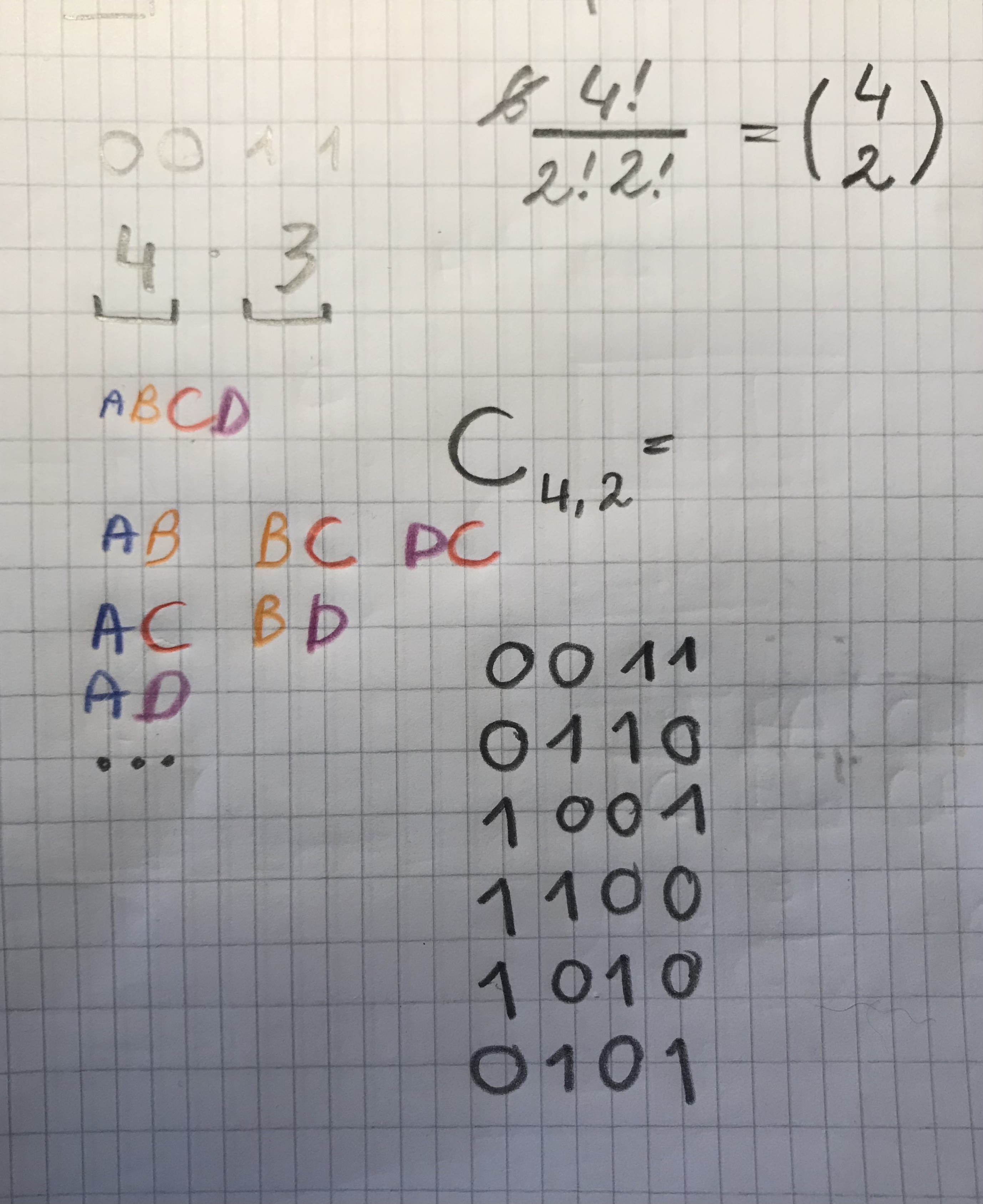
$8!\ggg 4! \implies \frac{8!}{4!4!} \ggg 1$
When I start calculating 12!/6!6!, I can cancel out the shared factor 6*5*4*3*2*1, but I don't see the patterns/meaning in cancelling out shared factors of 12*11*10*9*8*7 with 6*5*4*3*2*1. Then what if we need to think about 24!/12!12! ... ?
I am learning to think mathematically and find patterns, and I am curious about what patterns exist there, why do we have this abstract collection of symbols?
Why the arrangements of 0011 are the same as choosing two elements from ABCD?
How the the pattern of 4!/2!2!, 8!/4!4!, and 12!/6!6! translates to pebbles, chord progressions, or rhythm?
The question arised why I care about analogies, and to think in terms of pebbles, so I tried to show it. I will attempt to document this here, to produce the blog article, as my actionable lead measure, however imperfect it might be as it is.



The Core Standards of Math Practice
I revisit these questions and guidelines often, to test them against what I do, and to permute the ideas.
 Steve Strogatz in The Joy of X: A Guided Tour of Math from One to Infinity
Steve Strogatz in The Joy of X: A Guided Tour of Math from One to Infinity
I learnt that there is not one correct solution to any problem in mathematics, and that multidimensional thinking is very useful in solving problems, or thinking about problems. Often, from the connecting of different field of mathematics, and of different aspects of life solutions, or insight emerges. This is very relevant to mathematics, and not trivial.
I think first you have to make effort, and make many mistakes, and in the process find what works. If I understood the concept I would not spend time wondering about it. 8!/4!*4! is abstract, and it can be great to think abstractly about it, and it has its benefits. On the other hand, the concept of factorial, permutations, variations, and combinations are relevant to so many things, which can also be very intersting. These concepts seem to relate to all sorts of aspects in life, and they seem to be relevant. Certainly, these connections make mathematics interesting to me. You can connect abstract mathematical ideas, formulas to things that interest you, and this practice will help you understand the subject deeper. It will also create more motivation to study it further.
Maths has wide reaching connections, to art as well.
Analogies are highly relevant to mathematics, as far as I understand, with my layman understanding of mathematics.
I think it is useful to take two seemingly unrelated concepts, and bring them together, to gain mathematical insight into some problem.
(8*7*6*5)/(4*3*2*1)

How do 4^4 and 4! relate?
I am starting to see patterns! 🐠
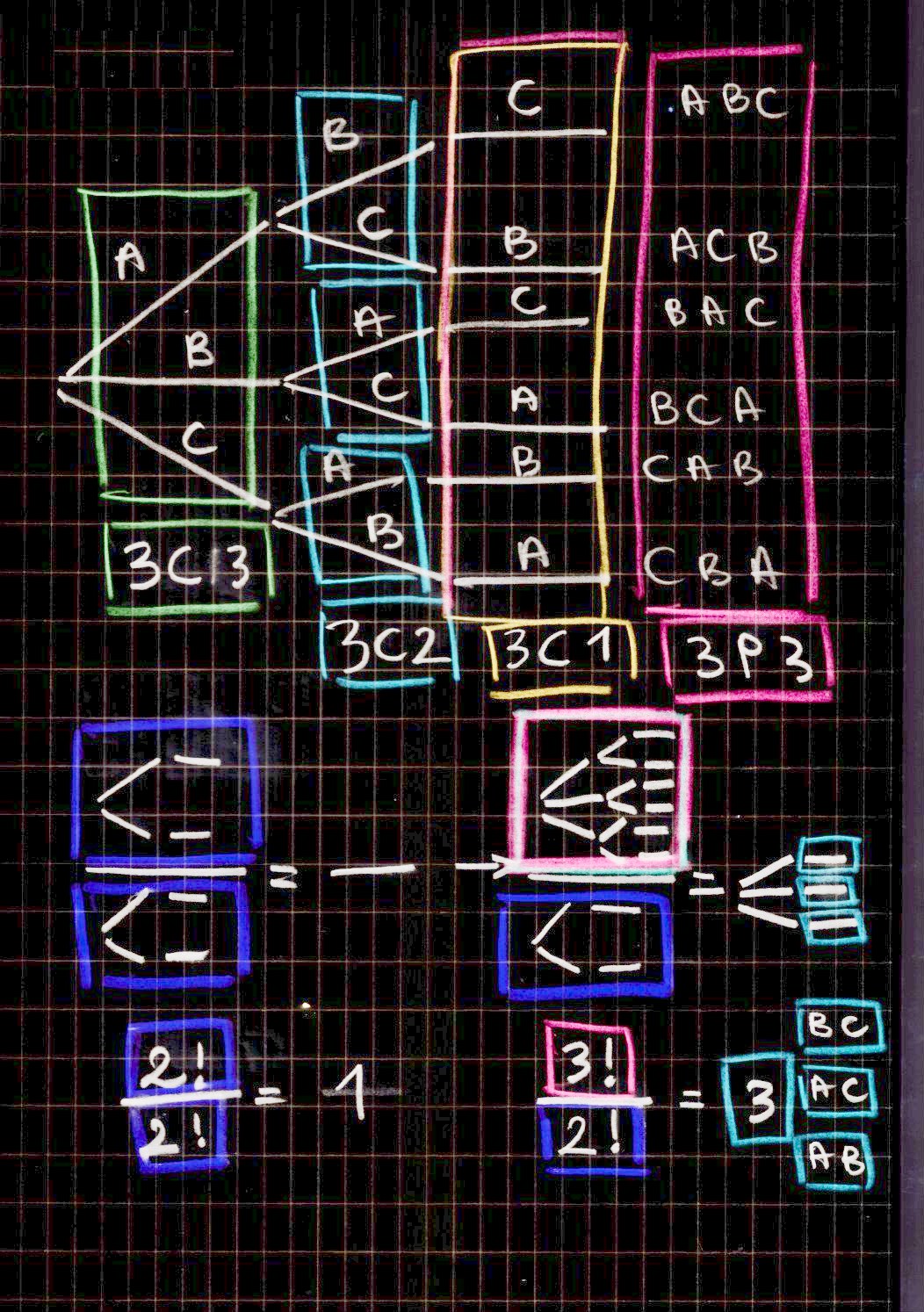
These are a few journal pages of my combinatorial fumbling:



- Previous: Permutations, combinations, variations
- Next: If you have ghosts