Diophantine equations, fostering algebraic questions
COMPAQ #
Combinations of "COMPAQ". I am learning questions from "Fostering Algebraic Thinking" by Mark Driscoll.

How does n! relates to (n-k)! in $V_{n, k} = \frac{n!}{(n-k)!}$?
 |
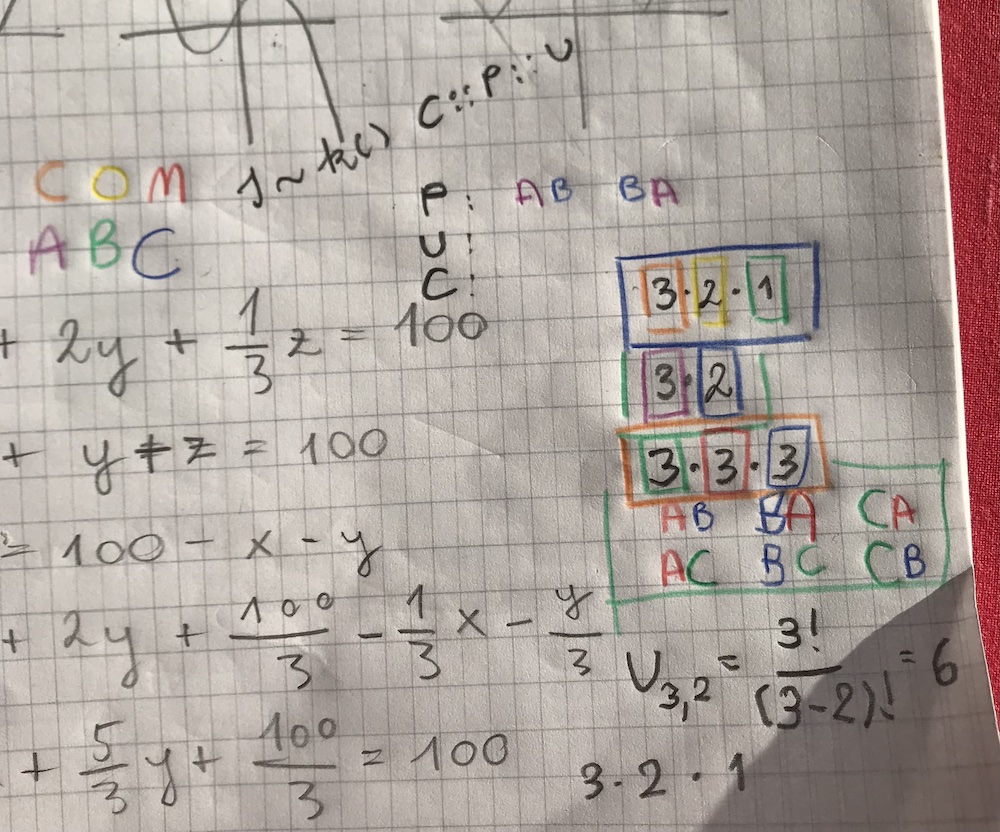 |
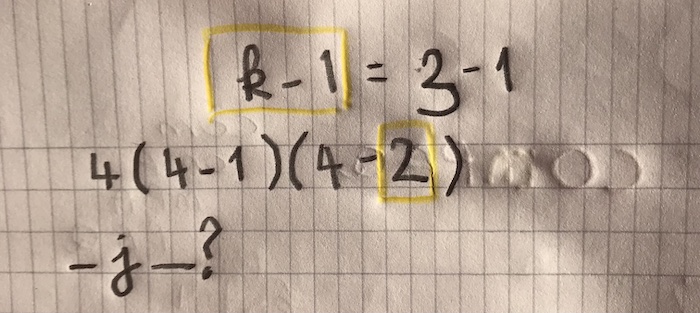 |
Compare combinations, permutations and variations.
How can I write the expression in terms of things I care about?
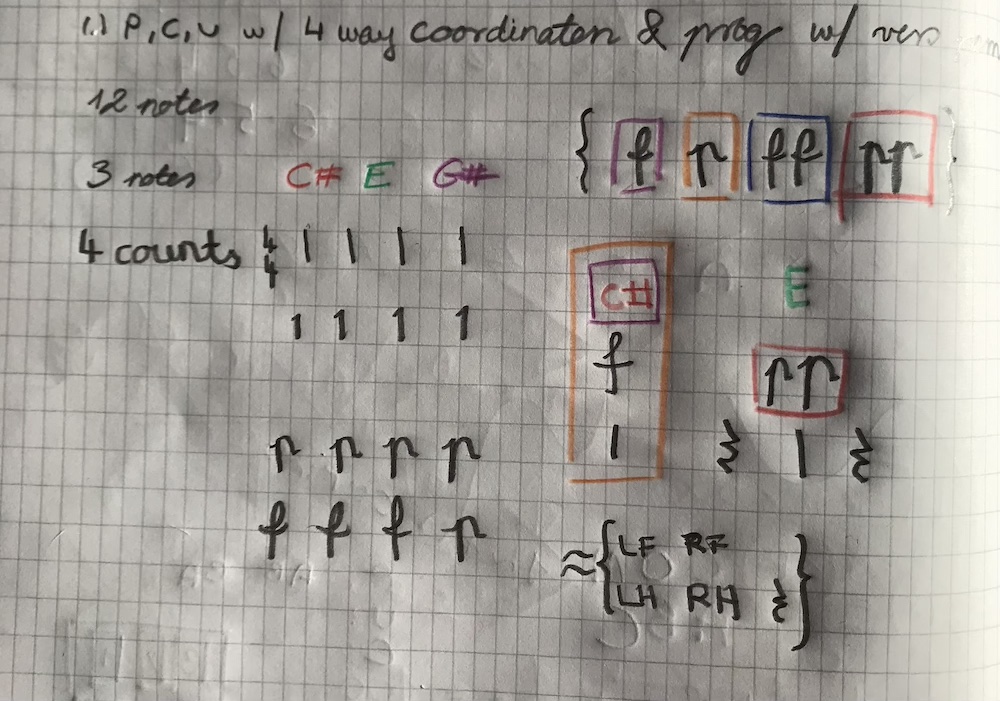
Pebbles, sunlight, leaves, jazz progressions, 4 way coordination, coloring pencils, watercolor.
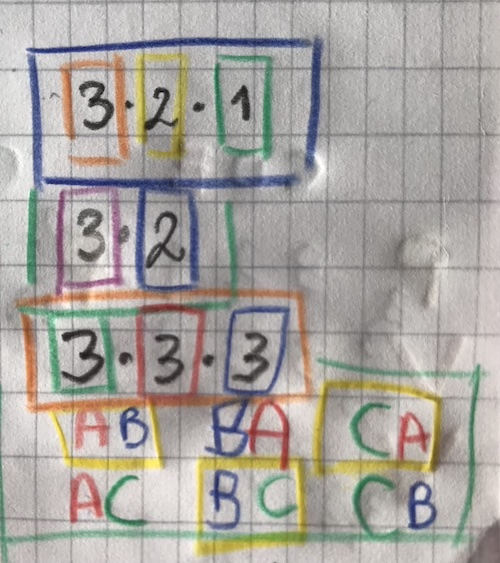
I am starting gain some understanding, and this is a good feeling! The color coding is not entirely meaningful, but it helps me to see patterns, and compare the concepts of permutations, variations, combinations with repeating or distinct elements.
 |
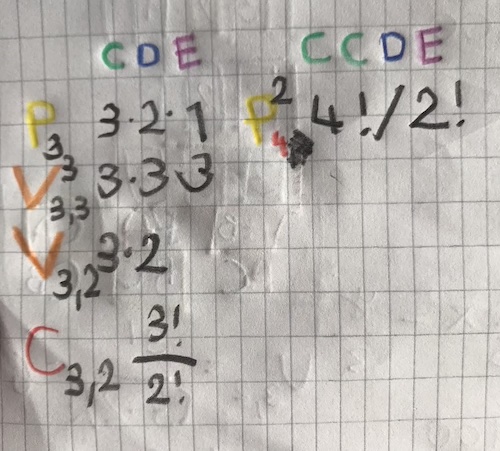 |
It's fascinating, I am fascinated by connections in maths, and the simple insight that I gain 👏.
I started from not knowing anything about permutations, variations, and combinations.
I am connecting it with algebraic thinking from the Mark Driscoll book.
Chord progressions
color coding
looking at simpler forms, and abstracting from things that matter to me, eg pebbles, jazz patterns, mathematics, I learn the concepts and make many connections. These connections seem to be very meaningful! Does the world speak the language of combinatorics? 🧬
"Visualise, play, investigate!"