Data Science Wizardry Blog by Attila Vajda

Sorting algorithms in vision

Algos book learning about sorting algorithm #

A beautifully sorted array of cells, orchestrating vision. Planning a movie marathon, and organising films by genre, release year or rating, is an idea of sorting in a real life scenario.

Sorting tones by pitches [C,D,E]. TonedEar What algorithm do I use to sort in this example? Several processes happen in our brains, related to auditory perception, pattern recognition, memory recall, and cognitive decision making. Computational techniques were inspired by these processes, because they can help recreate pitch detection.

Waffle Puzzle #

original_value = 17
for waffle_count in range(23, 10, -4):
    new_val = original_value + (waffle_count % 3 == 0) * (waffle_count // 2)
    original_value = new_val
print("The final result:", original_value)

This is good cognitive exercise for me! Lately I find value in spending time exploring basics. Solving this puzzle I practice, among other things, number sense, %, //, order of operations, updating variables, reading code, reading range() values, and using Boolean values as 0, and 1. It is quite complex.

Maths patterns of reasoning. $\forall ~ 3 | \text{waffle_count}$ ?

Is waffle_count always evenly divisible by 3? How to write this in a list of way please in maths notations?

(\forall k \in \mathbb{Z})(\exists m \in \mathbb{Z})\colon \mathrm{waffle}_\mathrm{count}(k)=3m

A waffle_count-ot bármelyik egész számmal megszorozhatom, mindig lesz egy olyan egész szám, amit hárommal szorozvan waffle_count-ot kapok.

We can multiply waffle_count by any whole number k, and there will be a whole number m that we can multiply by 3 to get waffle_count.

happy.

Practicing mahamudra throughout the day #

To boost my digestion I am practicing diaphragmatic breathing, and using the intercostal muscles. I also do 1-2 min sarvangasana, shirshasana, plow pose, etc. Furthemore, I drink plenty of water.

cs books whimsy #

Logistic Regression is a classification algorithm!

scikit learn 🍪 #

Metadata routing breaks MultioutputClassifier with estimator that doesn't support sample_weight in fit. #28239

Metadata routing issue analogies by Mixtral bot

Analogy 1 - Library Sorting:

# Assume we have two lists: one containing book names and another having categories
book_names = ['BookA', 'BookB', 'BookC']
categories = ['Fiction', None, 'Non-Fiction']

# We cannot directly use Zip operation here as there are missing entries
sorted_books = sorted([(name, cat) for name, cat in zip(book_names, categories) if cat])
print(sorted_books)

An ensemble classifier, harmonising predictive melody in an analytic composition. Multioutput Interlacing sample weight support, like missing instruments. Harmonising metadata routing. Each output requires precise handling. Alternative methods to accomodate missing arrangements. Finness of metadata routing, without sample weight support. Is it possible to have metadata routing without sample weight support? Managing information without routes. Crafting ways for information for efficient roads.

The equivalent in statistics is stratification. Categorising data to different groups. Specific pathways, targeted analysis, subgroups.

Sample weight is like drawing different lines with widths, to create emphasis. This visual analysis creates a nuanced and detailed understanding of the role of sample_weights in MetadataRouting. Sample weights show the significance of datapoints. Assigning levels of importance.

ZOONOOZ #

In the Obadovics Statistics book I came upon the task of permuting the word 'MATEMATIKA', and the equation

$$ P_n^{\left(k_1, k_2, \ldots, k_r\right)}=\frac{n !}{k_{1} ! k_{2} ! \ldots k_{r} !} $$

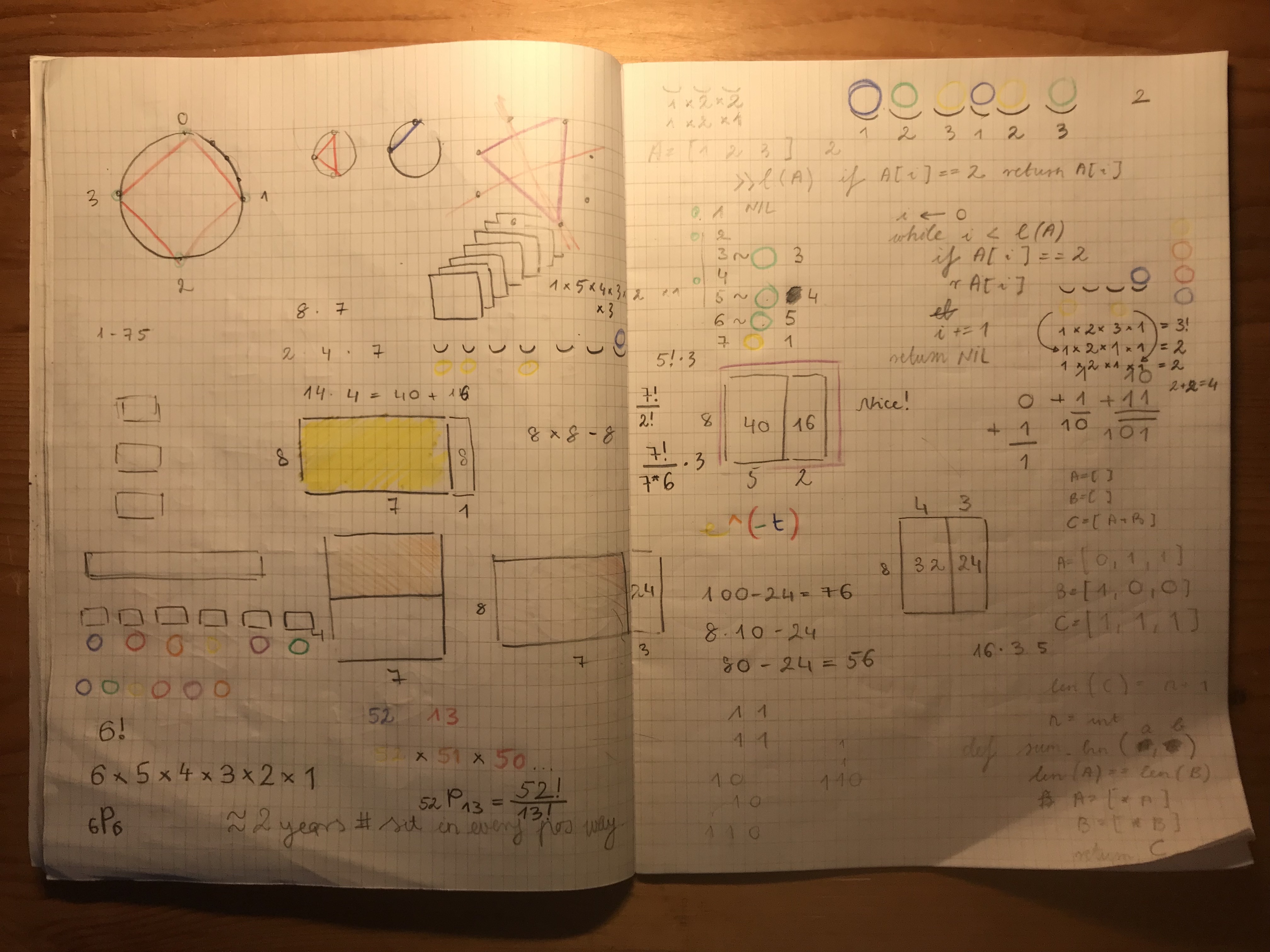
Permutations journal entry page

I found insight into what the equation means, and now I found the 'ZOONOOZ' task in the Harold Jacobs!

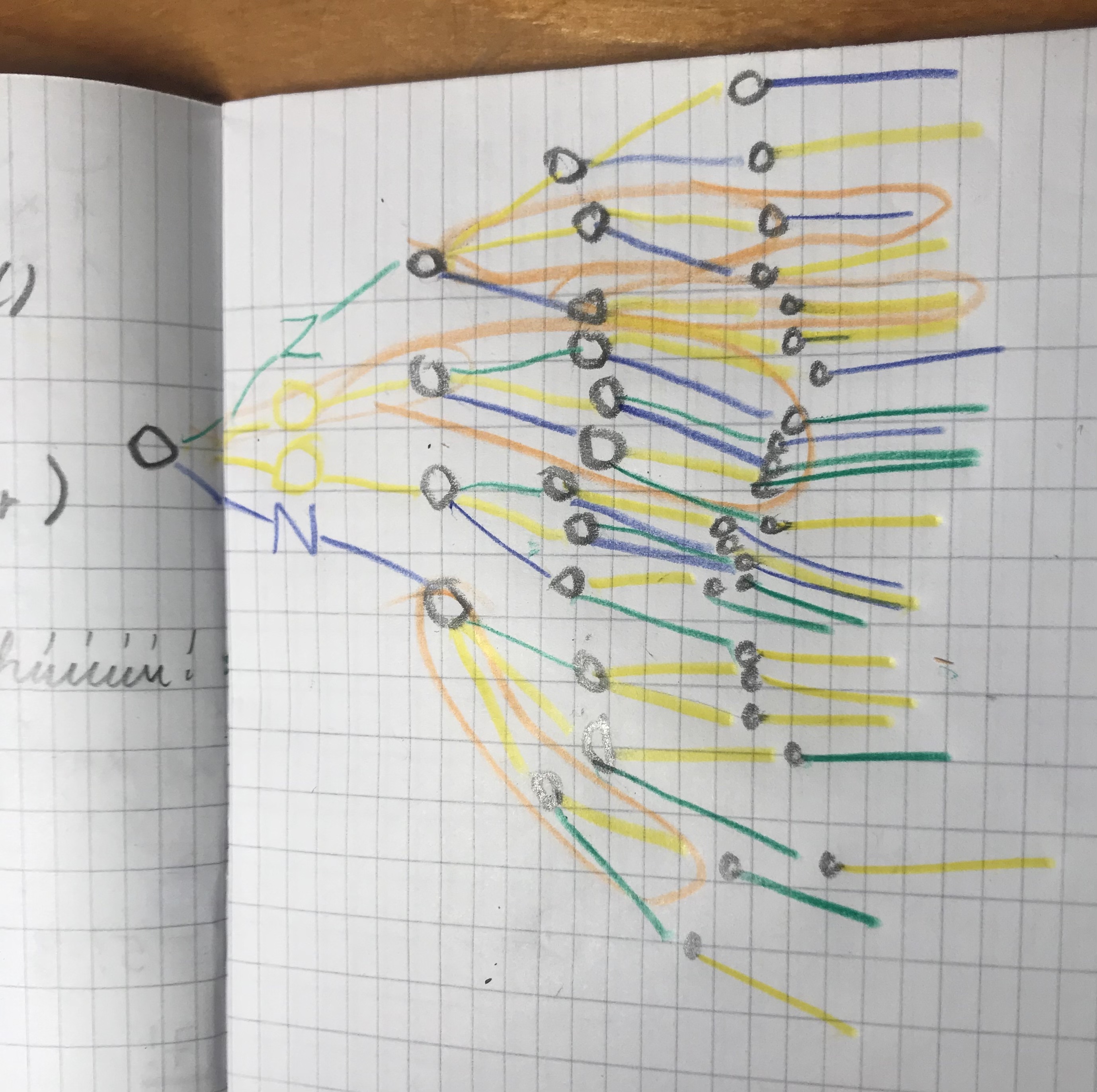
Color coded permutations of ZOON

Nice! We can label the letters $Z_1, Z_2, O_1, O_2$ etc. This is also an example of collaboration, learning from the perspective another person.

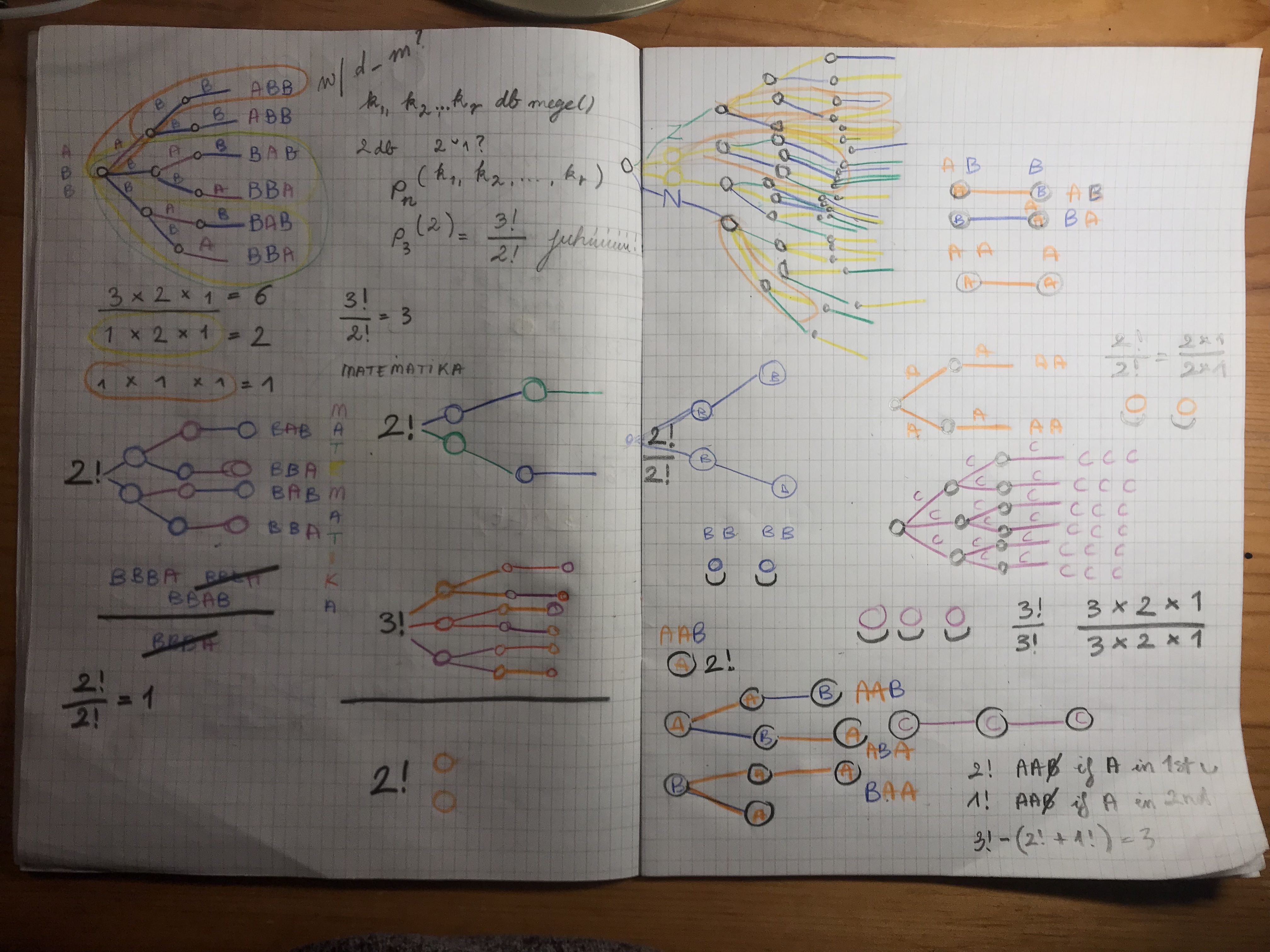
Fantastic! Collaboration is just wonderful. I asked on Discord, and got beautiful insight into this concept. I used to focus on the individual repeating elements, or letters, and now see, that entire branches of the tree diagram repeat, and they take one slot, or position of the diagram.

Very nice indeed! I struggle with the understanding. My attempts at drawing the simpler forms of the formula, to try to see what is happening:

Attempts at drawing the simpler forms