Data Science Wizardry Blog by Attila Vajda

Minus six degress, sunlight

Sum of two binary integers #

Vizsgáljuk meg azt a problémát, amikor összeadunk két n bites egész számot, melyeket két n-elemű tömbben, A-ban és B-ben, tárolunk. A két egész összegét bináris formában kell tárolni egy (n + 1)-elemű tömbben. Fogalmazzuk meg a problémát formálisan, és írjunk pszeudokódot a két egész szám összeadására.

.stniop owt neewteb ecnatsid tsetrohs eht gnidnfi seriuqer taht eno ebircseD.gnitrosseriuqertahtelpmaxedlrow-laernworuoyebircseD

≈ 71kg my own bodyweight 24kg kettlebell 16kg kettlebell 8kg kettlebell 5kg medizine ball 2kg medizine ball ≈8.56 oz (243 g) beach volleyball

-?gnittes dlrow-laer a ni redisnoc ot deen uoy thgim ycneicfife fo serusaem rehto tahw ,deeps naht rehtO 2-1.1

Algorithms task

$a=\sum_{i=0}^{n-1} A[i] \cdot 2^i$,

I don't yet know what this means.

def binary_representation(arr):
    result = 0
    for i in range(len(arr)):
        result += arr[i] * (2 ** i)
    return result

# Example usage:
arr = [1, 0, 1, 1, 1, 1, 1, 1, 1, 1]
print(binary_representation(arr))  # Output: 1023

All of my fingers are open, 10 1s, or 1111111111 = 1023 -> [1, 0, 1, 1, 1, 1, 1, 1, 1, 1] ≠ 1023

Structure is the organistion and arrangement of components within the code, or algorithm. Logic refers to the reasoning behind the steps taken in the code, or algorithm. Syntax refers to the specific rules and conventions used in the code, or algorithm.

Nice, a is the decimal representation of a binary number, because we iterate over the digits of the binary number, and sum 2-s taken to the power of the digits.

a represents the base 10 interpretation of a binary number. The calculation a converts a binary number to its corresponding decimal value.

Why do we multiply by two raised to the power of its position index?

This is wonderful, because I learn what i means in the formula. n-1 is the last digit The position index of the last digit. A[i] is the digit at i position index We sum digits of A, starting at position index 0, ending at the last digit at position index n-1. Digits of A multiplied by 2 to the position index of the digit.

I am now trying to figure out what the building blocks of this algorithm are.

>>> bin(42)[2:]
'101010'

This function should only take a binary integer or a string of a binary number, I think.

def add_bin(a, b):
    # Check if inputs are either integers or strings
    if not (isinstance(a, (int, str)) and isinstance(b, (int, str))):
        raise ValueError("Inputs must be binary integers or strings")

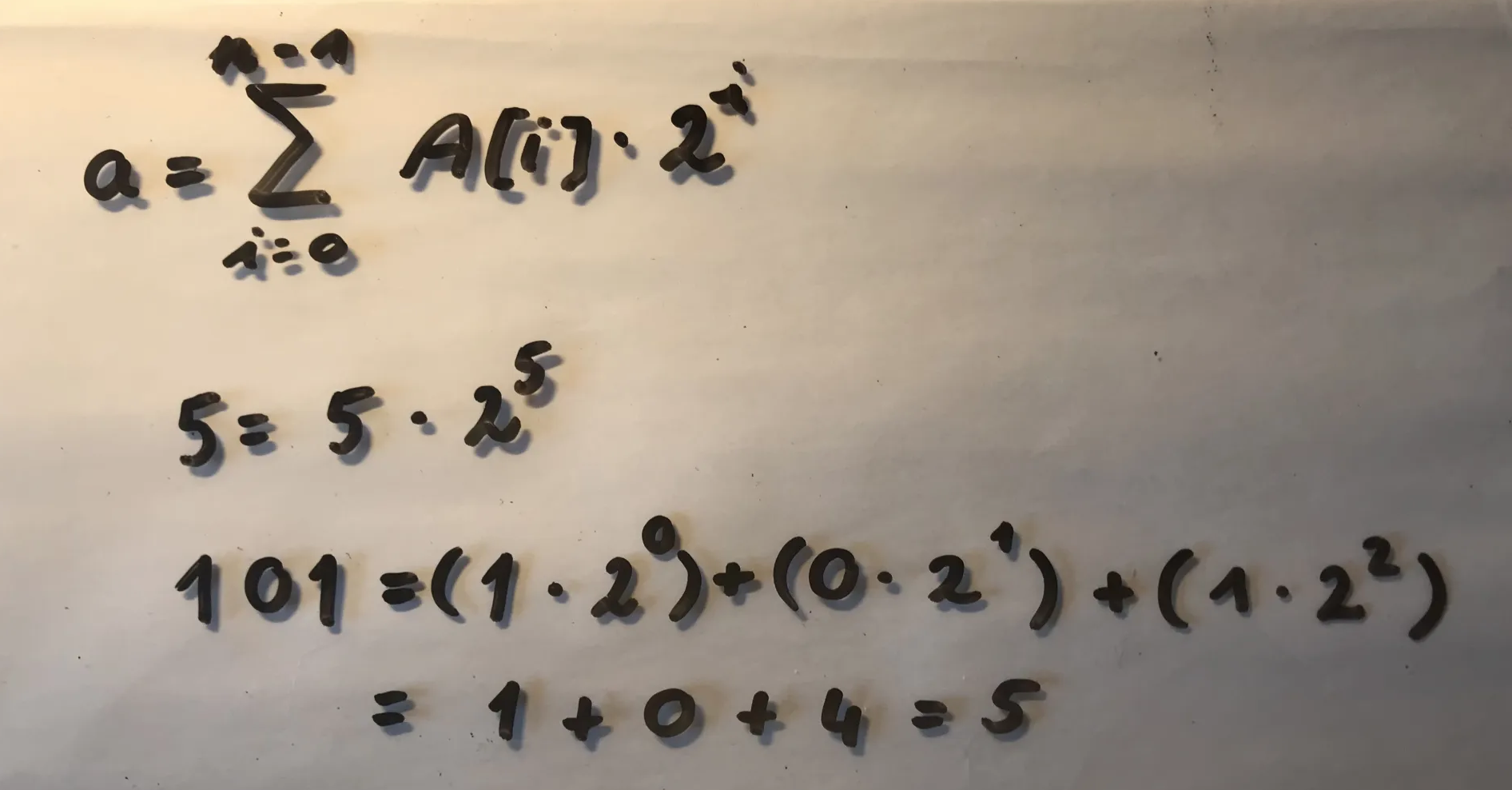
a and b are not base ten inputs, as I believed, but are n bit binary integers: Testing the formula of with plugging in 5, and 101

def sum_bin(a,b):
    return bin(a+b)[2:]

print(sum_bin(a,b))

A simple way to write it is:

bin(a+b)

The implementation of bin in the Python codebase, in C, is:

static PyObject *
builtin_bin(PyObject *module, PyObject *number)
/*[clinic end generated code: output=b6fc4ad5e649f4f7 input=53f8a0264bacaf90]*/
{
    return PyNumber_ToBase(number, 2);
}
def add_bin(a,b):
    n = len(a)
    A, B = [*a], [*b]
    C = [0] * (n + 1)
    carry = 0
    for i in range(n-1,-1,-1):

print(add_bin("1", "1"))
>>> n = 5
>>> *range(n-1,-1,-1),
(4, 3, 2, 1, 0)
a = "101011"
A = [int(digit) for digit in a]

print(A)

This is something I struggle with! 🎉😌 % and // are relevant to this task. The algorithmic thinking in terms of carry, modulo, //, arrays, conditions and data structures.

def add_bin(a,b):
    n = len(a)
    A = [int(digit) for digit in a]
    B = [int(digit) for digit in b]
    C = [0] * (n + 1)
    carry = 0
    for i in range(n-1,-1,-1):
        C[i+1] = (A[i] + B[i] + carry) % 2
        carry = (A[i] + B[i] + carry) // 2
        C[i] = carry
    return {"A": A, 
            "B": B, 
            "C": C}

print(add_bin("111", "111"))

{'A': [1, 1, 1], 'B': [1, 1, 1], 'C': [1, 1, 1, 0]} 👏

We can use divmod to simultaneously compute the quotient and the remainder:

for i in range(n - 1, -1, -1):
        carry, C[i + 1] = divmod(A[i] + B[i] + carry, 2)

The final solution to the problem, testing for binary inputs, and padding numbers for same length:

def add_bin(a,b):
    if not all(bit in '01' for bit in a + b):
        raise ValueError("Inputs must be binary strings.")

    # Make the inputs the same length with paddings
    n = max(len(a), len(b))
    A = [int(digit) for digit in a.zfill(n)]
    B = [int(digit) for digit in b.zfill(n)]

    C = [0] * (n + 1)
    carry = 0

    for i in range(n-1,-1,-1):
        C[i+1] = (A[i] + B[i] + carry) % 2
        carry = (A[i] + B[i] + carry) // 2
        C[i] = carry

    return {"A": A, 
            "B": B, 
            "C": C}

print(add_bin("111111", "111"))

{'A': [1, 1, 1, 1, 1, 1], 'B': [0, 0, 0, 1, 1, 1], 'C': [1, 0, 0, 0, 1, 1, 0]}

Metadata Routing breaks ColumnTransformer #28186 #

Metadata Routing breaks ColumnTransformer #28186

Metadata routing is like keeping track of changes to data in a game of telephone.

Mixtral description of MetadataRouter

Asking computer agent to explain components of a code in terms of analogy works very well in accessing difficult language.