Data Science Wizardry Blog by Attila Vajda

Granularity of dreams

Buddhas of compassion #

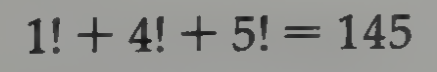
1!+4!+5!=145

I struggle with 8*7, 64-8=56

18 x 5 from youcubed on Vimeo.

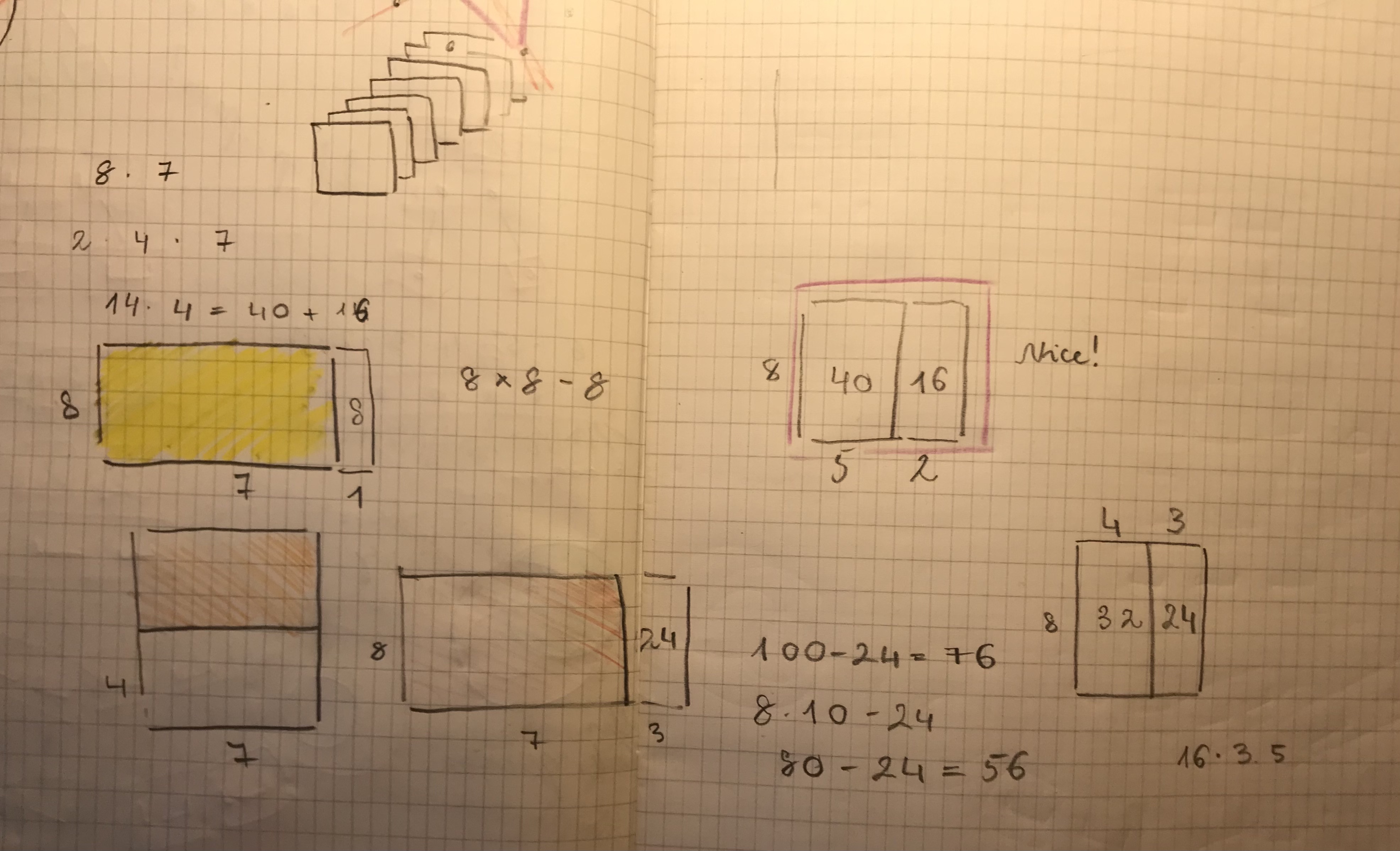
Visual representations of number sense calculations of 8*7

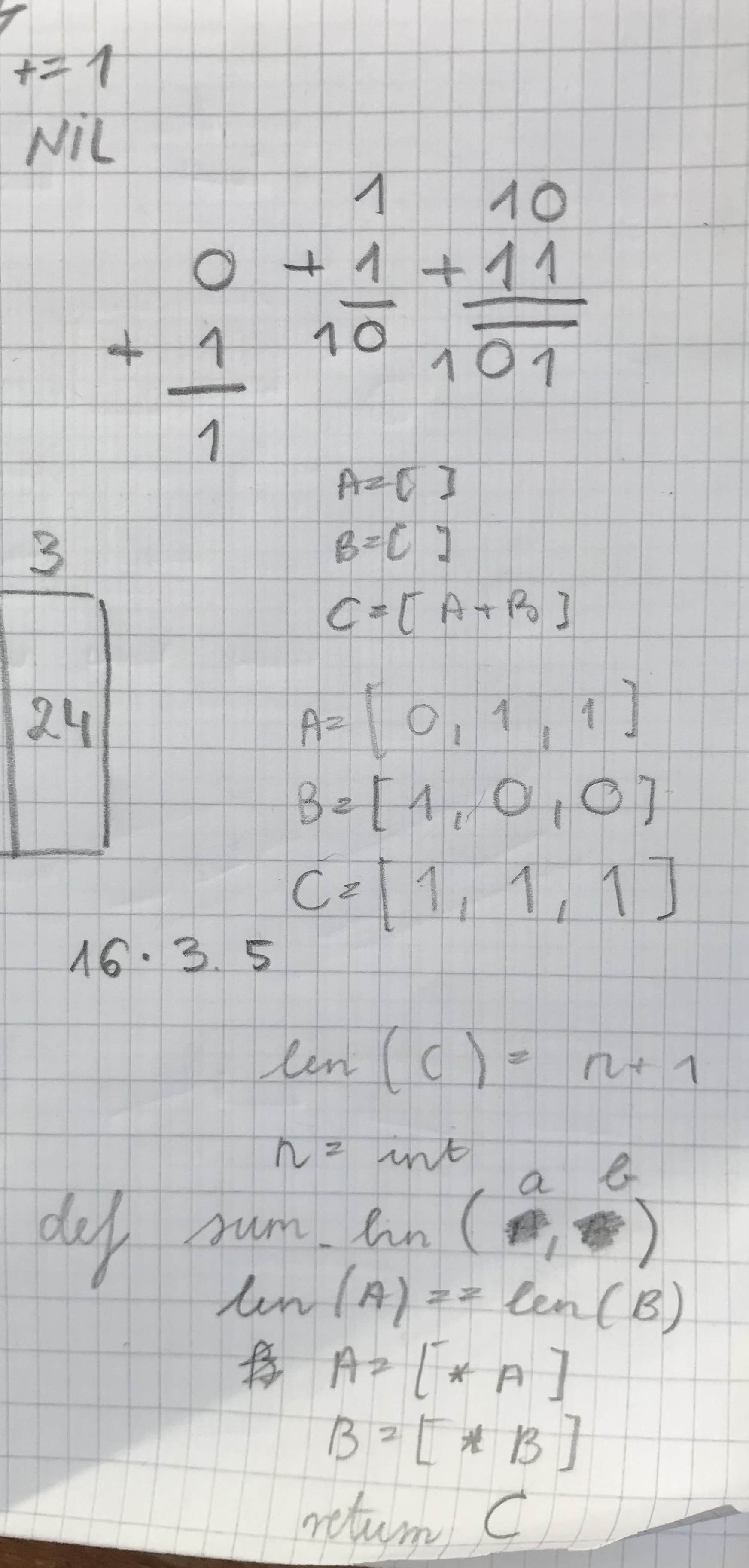
Save two equal length binary numbers in lists A, and B, and return their sums in a list C. #

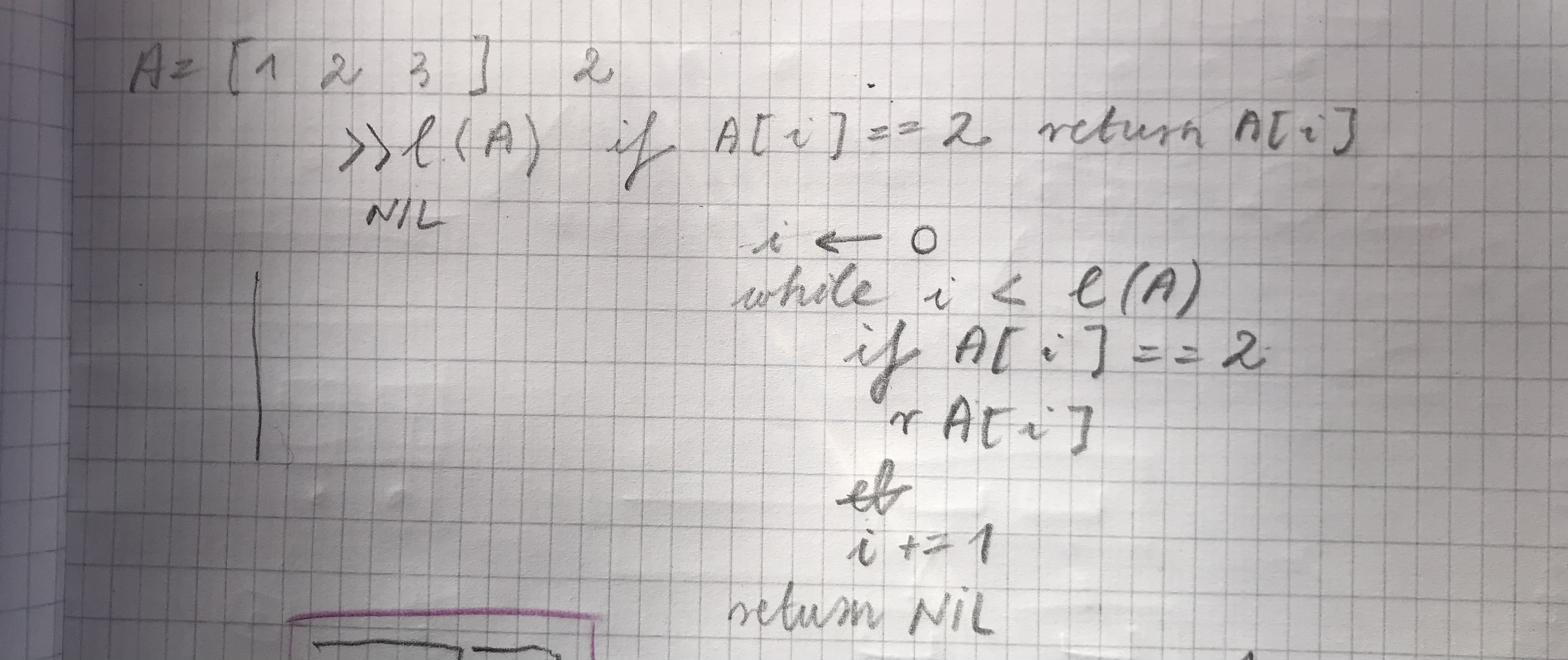
sketch for algorithms task Sketch for algorithms task in pencil

>>> sum_b = lambda a, b: str(a).startswith(0b) and str(b).startswith(0b) and len(str(a)) == len(str(b)) return [*str(a+b)]
  File "<stdin>", line 1
    sum_b = lambda a, b: str(a).startswith(0b) and str(b).startswith(0b) and len(str(a)) == len(str(b)) return [*str(a+b)]
                                            ^
SyntaxError: invalid binary literal

Equation I am figuring out #

$$ P_n^{\left(k_1, k_2, \ldots, k_r\right)}=\frac{n !}{k_{1} ! k_{2} ! \ldots k_{r} !} $$

🍊🍊💡💡❤️❤️
6!/2!2!2!

🧬🐍
2!/1!1! = 2

💾💾🖊
3!/1!1! = 6/1 = 6
💾💾🖊, 💾🖊💾, 🖊💾💾
💾💾🖊, 💾🖊💾, 🖊💾💾

Code puzzle frequency #

frobnitz = 0, 1, 2
blargh = [frobnitz]
blargh.append(3)
blargh.pop(0)
print(len(blargh))
quuxle = (0, 1, 2)
snorkel = [quuxle]
for i in range(len(quuxle)):
    quuxle[i], quuxle[-i - 1] = quuxle[-i - 1], quuxle[i]
snorkel.append(3)
snorkel.pop(0)
print(len(snorkel))

This is an outstanding puzzle! quuxle = [0, 1, 2] is an option.

flarb = 'gizmo'
if len(flarb) > 0:
    result = sum([flarb.find(char) for char in ['q', 'x']]) + flarb.count('')
else:
    result = 0
print(result)

👏

-10 Whimsy points for me.

rfind()

result = sum([flarb.rfind(char) for char in ['q', 'x']]) + flarb.count('')
print(result)
>>> flarb = 'gizmo'
>>> flarb.count('')
6

This was my intuition, but I guessed 1, for a '' at the beginning of the string.

scikit-learn farble #

Regression in k-neighbours with sparse data #28191

Identifying bottlenecks, to reduce unnecessary computations. The reduction in the execution time of the kneighbors method for sparse matrices, and ensuring compatibility across different versions of scikit-learn.

Anagram test algorithm #

def is_anagram(a, b):
    if len(a) != len(b):
        return False
    a = sorted(a)
    b = sorted(b)
    for i in range(len(a)):
        if a[i] != b[i]:
            return False
    return True
is_anagram = lambda a, b: sorted(a) == sorted(b)
is_anagram = lambda a, b: all(e in b for e in a) and all(e in a for e in b)

This algorithm checks if two words have the same letters.

  1. Mayer, C. (2020). Python One-Liners. No Starch Press.

  2. Mayer, C., Rieger, L., & Chan, A. (2020). "Coffee Break Python - Mastery Workout: 99 Tricky Python Puzzles to Push You to Programming Mastery.".

  3. Cormen, T., Leiserson, C., Rivest, R., & Stein, C. (2009). Introduction to Algorithms. MIT Press.