Data Science Wizardry Blog by Attila Vajda

Classic probability space

I like this #

Kombinatorikai összefoglaló. A klasszikus valószínáségi mező eseményeinek valószínűségei általában kombinatorikus módszerekkel számíthatók ki.

"A summary of combinatorics. Probabilities of events of the classic probability space can be computed with combinatorics methods." Gyula J. Obádovics

This is from "Probability and Statistical Mathematics" by Gyula J. Obádovics

I'm reading and doing the tasks in this book, because I really like the textbooks of Gyula J. Obádovics.

practices that worked #

Python learning bout #

2h learning bout of 4*24min.

Inbetween I did a 10-15 min sitting meditation, with 5 minutes of cyclic physiological sigh, with the cat sitting on my leg 🐈‍⬛🧘‍♂️. All the way using the blog writing. I often would go days, or even weeks without attending to things that I wanted to do, so this practice answers this need. I had the notion that I had to wait until contributing to open source. For example, first I had to work my way through many books, and perhaps in a few months, or a year, I would be able to contribute. Now, I realised that I can do 10-20 minutes of contribution, or learning to contribute, and it is very beneficial. It was also satisfying to have done this.

Creative harmony with closed eyes #

Practicing the four seventh chords on the piano used to feel a bit boring. Yesterday I closed my eyes, and tried to play the chords with eyes closed. It was beautiful. I used one hand to step from one major 7 four chord to the other, in descending perfect fourths. Also, it was in a time of dark exposure, so I felt relieved from not having use artificial lights.

This practice allows for many mistakes, engages neuroplasticity, gives a new perspective to the understanding of the instrument. Introduces and grows the sense of touch. It feels great knowing where the keys are just by moving my arms there. Somehow this practice creates more emphasis on how chords sound. I would play a random combination of notes, and then try to find, perhaps C major 7 from that initial guess. It creates a sense of comparison, "these notes sound like this, and I feel these keys with my fingers, and then I alter it, now I play a 7th chord on the C major scale, now I move through the C major scale, and those steps have functions, and there is a sense of direction towards the tonic note."

This is an awesome book for harmony, so I am learning with this book:

it's the twigs, not the containers #

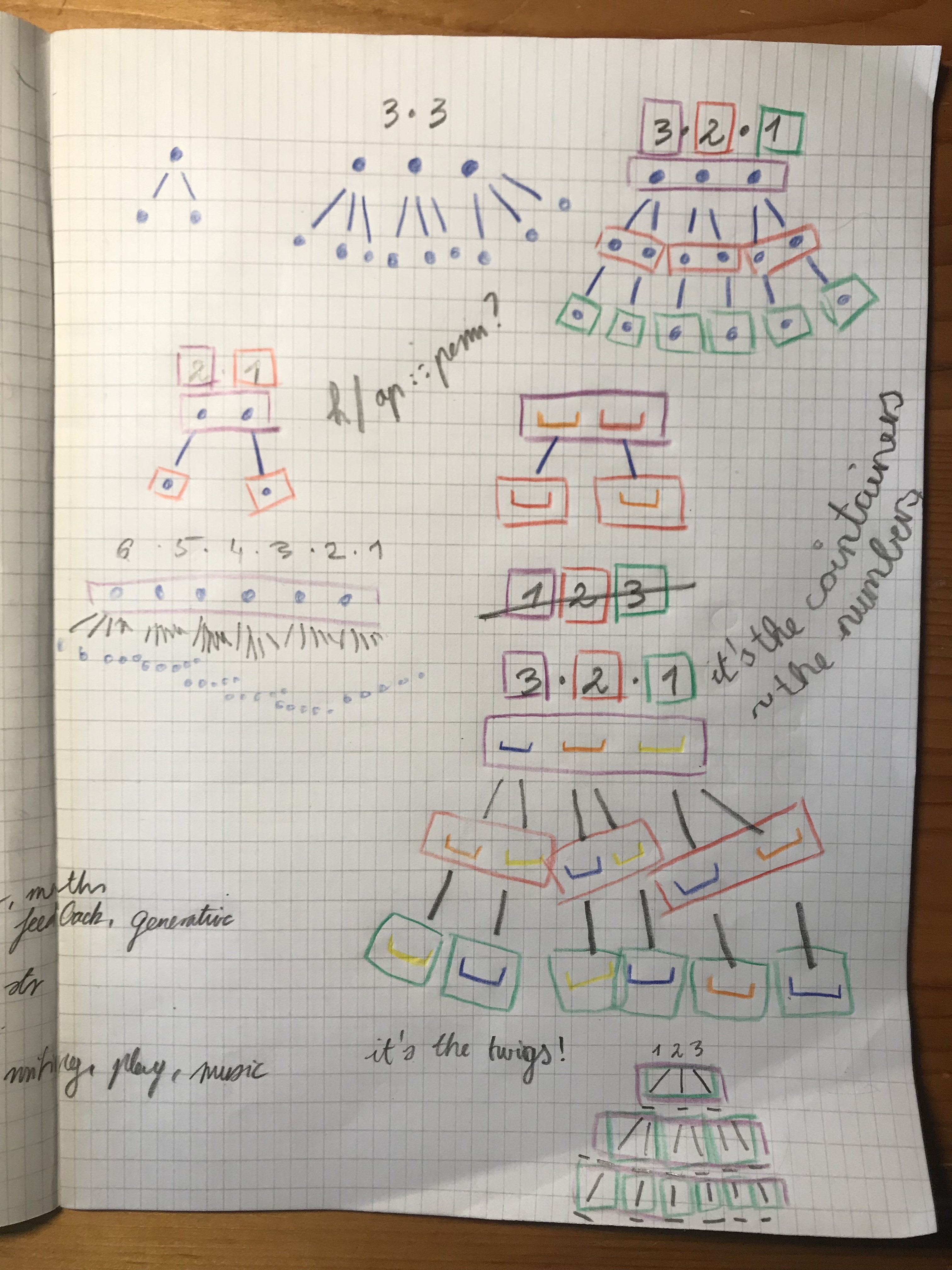
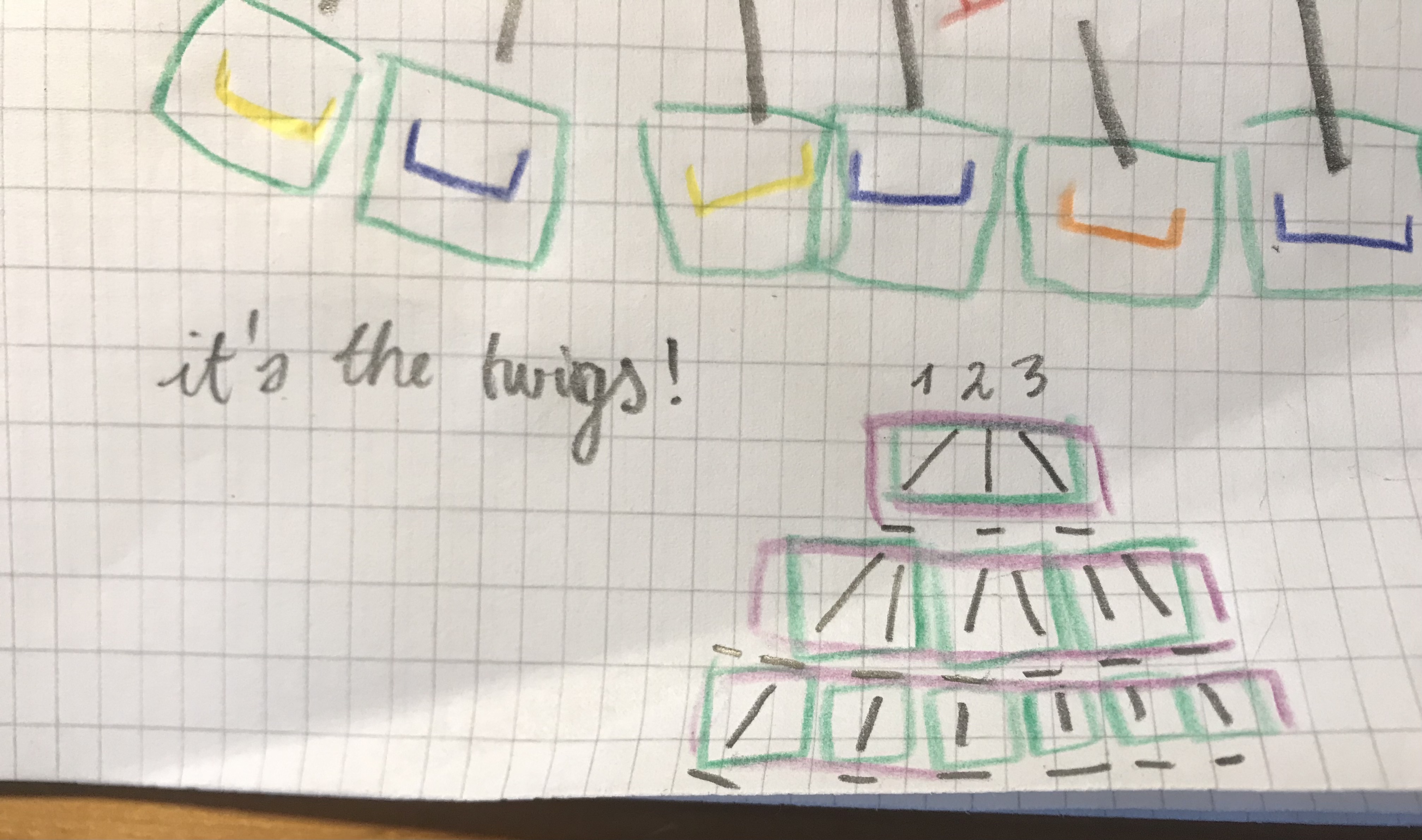
Visualising permutations Drawing showing that the permutations are visible in the branches of a tree diagram

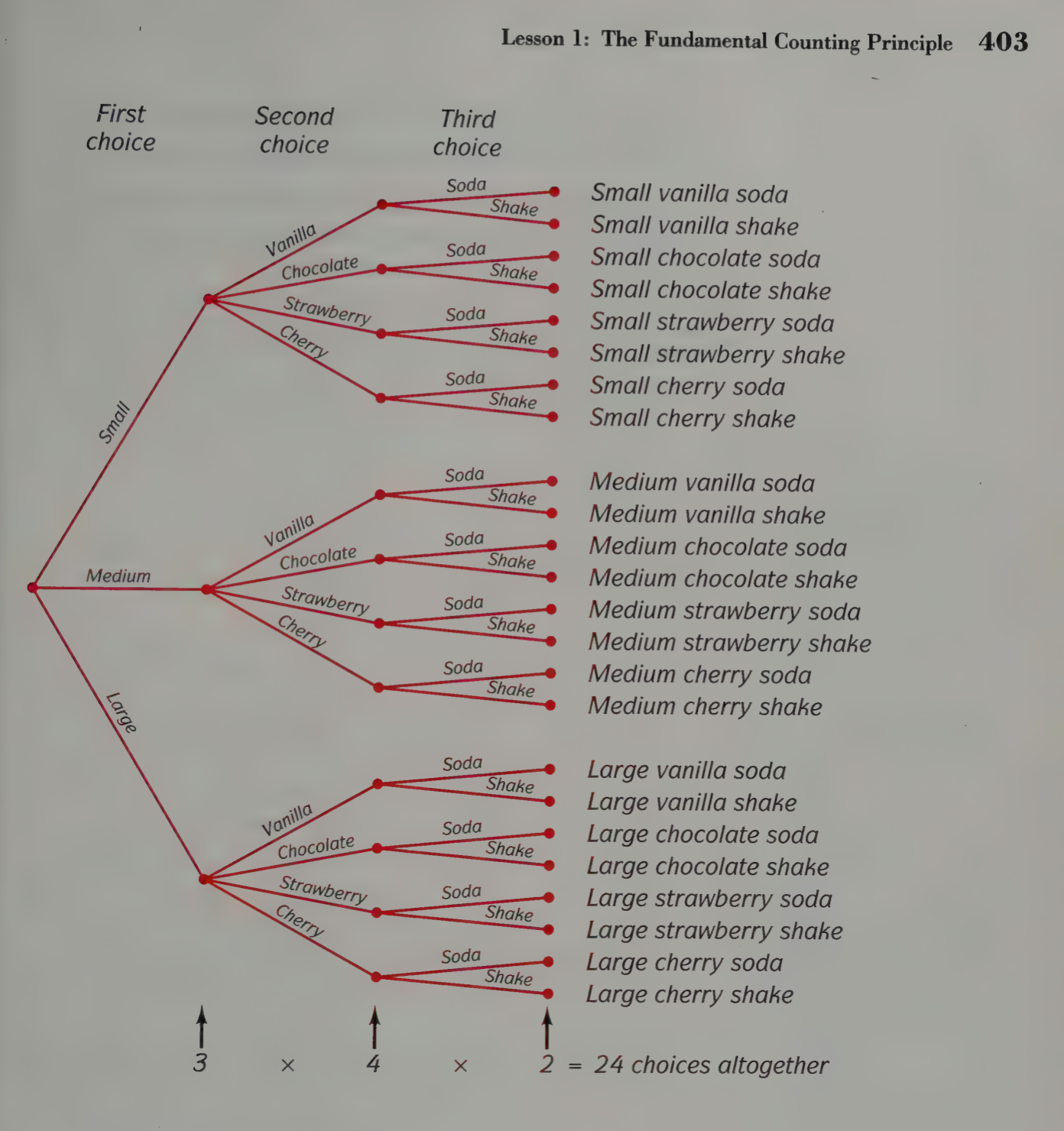
Wow, it's (Monty Python's Flying Circus) the the fundamental counting principle! Harold Jacobs in Mathematics, a Human Endeavor introduces permutations with tree diagrams, similar to the ones I drew.

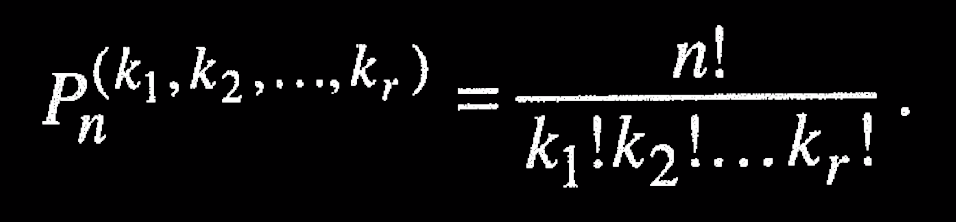
I revisited this book, to continue it, because I don't understand the abstract formula: Formula for repeating permutations

Why do we divide by the factorial of the product of the number of repeating elements? Where is this visible in permutations? I really liked the insight of seeing the actual pattern of 3*2*1 apparent in the branches of the tree diagram. Before seeing the branches, factorial was just a symbol to me 3!, I knew it meant 3*2*1, but I had no clue how it connected to permutations.

16 words end with letter T: 4 * 4 * 1 len('ACGT') * len('ACGT') * len('T') 🧬

1 * 4 * 1 letters start and end with the letter A!

If the genetic code was two letters long, 4 * 4 different words would be possible.

Tree diagram of ice creams choice

code puzzling #

texto = 'the zebra crossed the street cautiously during dawn'
guffaw = texto.count('the') < 2
print(guffaw)

This is interesting:

>>> isinstance(True, int)
True

I knew that True evaluated to 1, but I was unaware True was int. True belongs to the bool subclass of int. True ∈ bool, bool ⊂ int.

False ∈ bool ∧ True ∈ bool ⟹ {False, True} ⊆ bool

bool ⊂ int

Scikit-learn Exception in LogisticRegressionCV #28178 #

Exception in LogisticRegressionCV #28178

Please give appositives of Predicted and ground truth tables, minority classes, training or validation sets, cross-validation. How do these concepts relate to important statistics concepts?

Predicted tables are estimated output. The actual observed output, or ground truth table, is used to evaluate performance. Minority classes are fewer instances in a categorical variable. Cross validation is dividing data into multiple segments.

Prediction and estimation; understanding distributions and frequencies; data splitting methods; evaluation measures; overfitting prevention and bias-variance tradeoffs are a few relevant statistics concepts.

"Assigning negative infinite probabilities to absent classes" is like assigning zero books borrowings to unchecked titles.

Please put this issue and solution in 5 different analogical contexts.

Imagine having a basket of bananas, cherries, dates, and persimmons. You ask someone to arrange different fruits in separate baskets. They don't know about cherries, so they create three baskets with bananas, dates, and persimmons but leave cherries aside.