Data Science Wizardry Blog by Attila Vajda

Visualising permutations with Molly

permutations #

Where is 3!, 1*2*3 visible in the permutations of 123?

123
132
213
231
312
321

Why do we use 1*2*3?

I asked this question on Discord, and found that arranging 123 is similar to arranging pebbles in containers, but I don't yet see how! Here are a few, failed attempts at visualising it: Attempts at visualising permutations

Thinking hard, staring at the proof: Molly cat took a seat on the maths notebook, she stares at coloring pencils, dice, and coins.

I made progress, so I am happy!

I tried figuring out why permutations of "123" are expressed by 3*2*1, 3!, or 3 factorial. In other words where is 3*2*1 apparent in arranging the digits 1, 2, and 3. After asking around, and a few failed attempts at visualising it, I am beginning to understand it! It's like arranging pebbles.

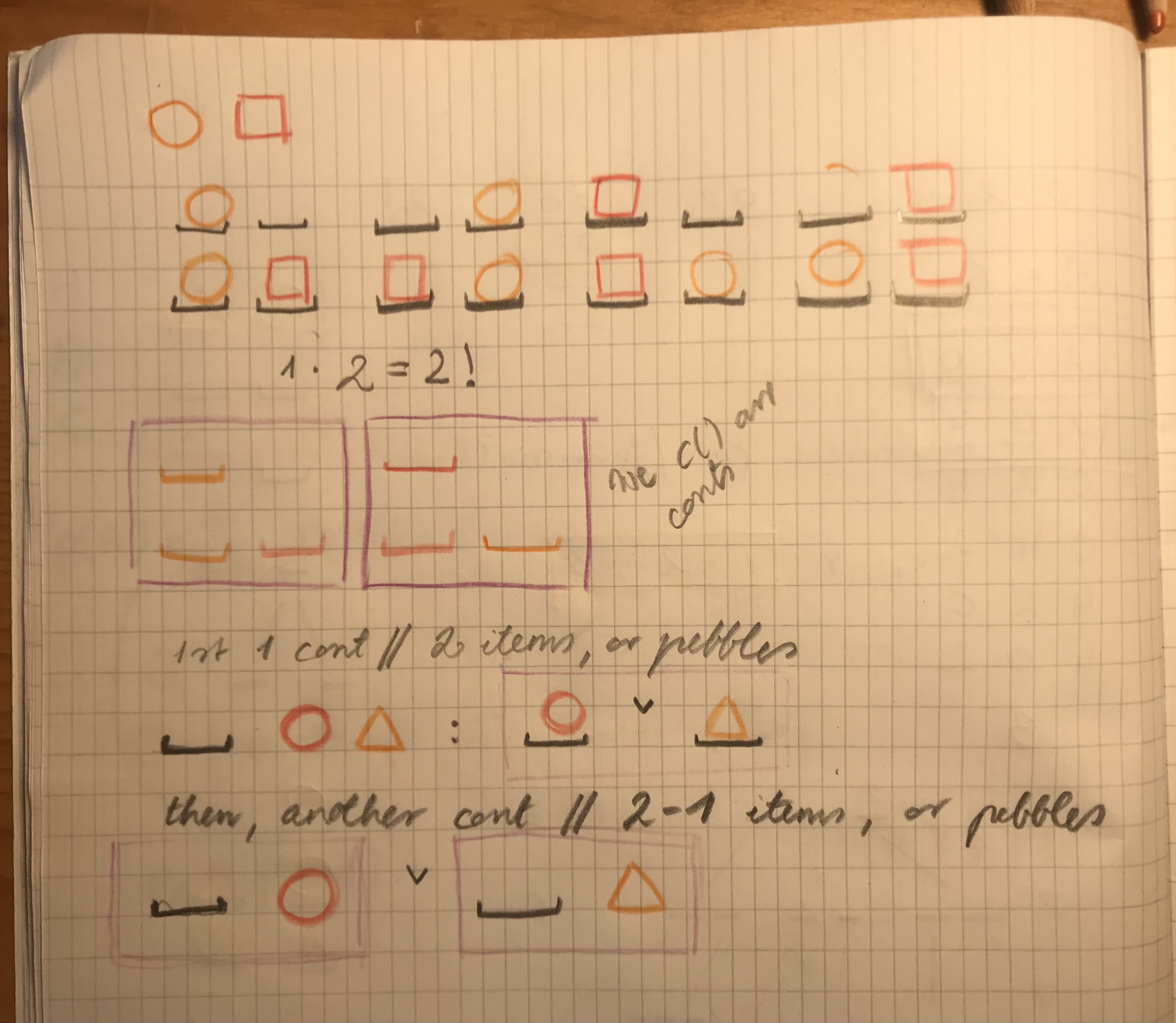
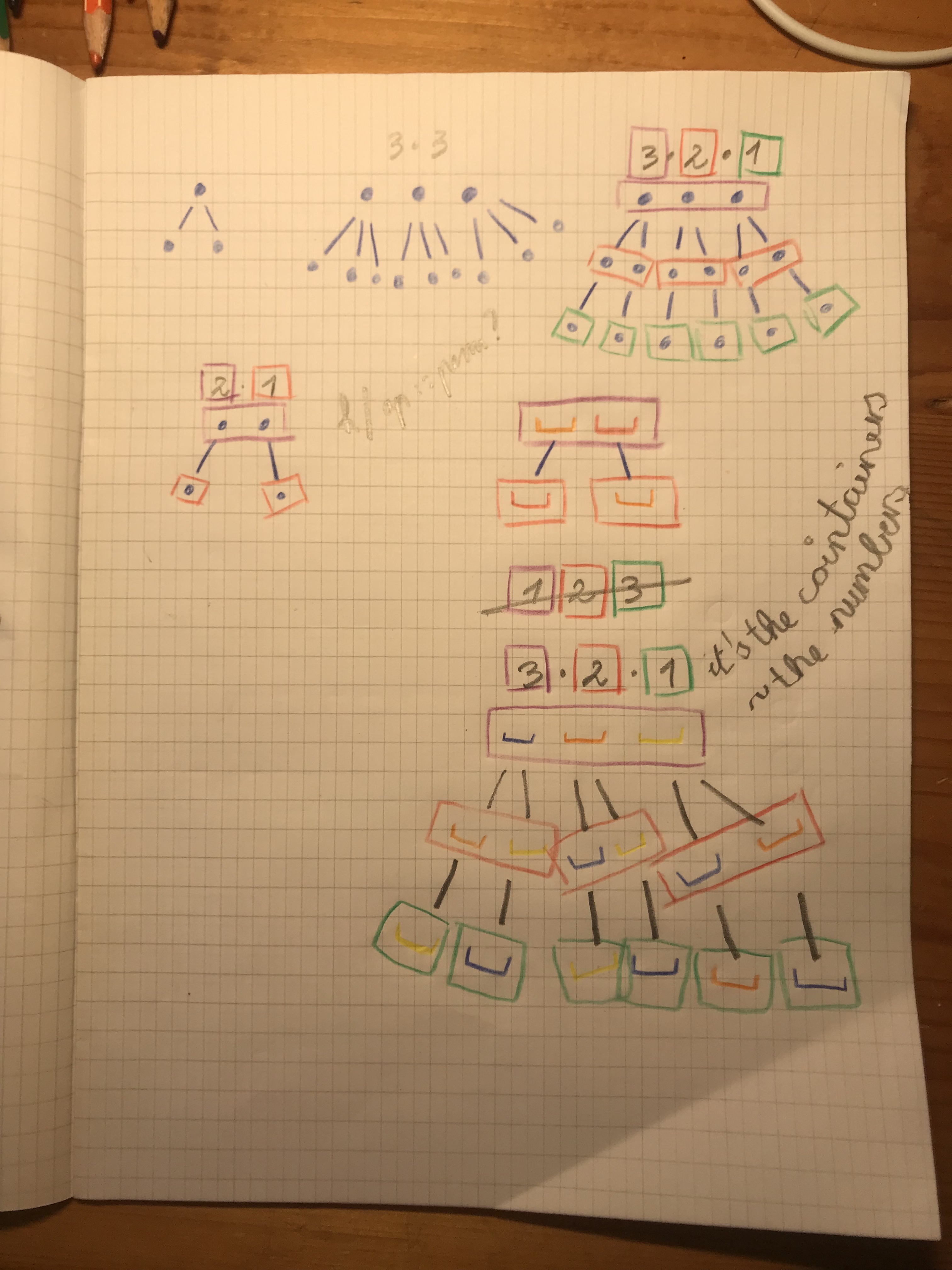
Visualising with containers, and colorful shapes Tree visualisation, diagram of permutations

Why, it's all pebbles and twigs!

code puzzle whimsy #

TARGET(FLUFFY_BUNNY) {
    frame->hop_location = bounce_around;
    bounce_around += 1;
    INSTRUCTION_PLAYFUL_STATS(FLUFFY_BUNNY);
    PyObject *carrot_field;
    carrot_field = skydiver[-1];
    int magic_carrot_count = 1 + (parachute_arg & 0xFF) + (parachute_arg >> 8);
    PyObject **cloud_top = skydiver + magic_carrot_count - 1;
    int joy_result = _PyEval_UnpackEnchanted(t_state, carrot_field, parachute_arg & 0xFF, parachute_arg >> 8, cloud_top);
    Py_DECREF(carrot_field);
    if (joy_result == 0) goto sadness_error;
    SKYDIVER_GROW((parachute_arg & 0xFF) + (parachute_arg >> 8));
    TAKE_OFF();
}

"What are we talking about here?"

`TARGET(FLUFFY_BUNNY) is a C macro, a preprocessor used to define pieces of code, that get expanded during compile time.

alpha = 42
bravo = {'omega': 0, 'zeta': 43}
alpha = 43
print(bravo[alpha])

What is the output of this code snippet? {'zeta': 43}

The output is KeyError: 43, because bravo does not have a key defined for 43.

>>> bravo[43]="Ford Prefect"
>>> print(bravo[43])
Ford Prefect

scikit learn sketch #

RFC: Towards reproducible builds for our PyPI release wheels #28151

A possible actionable lead measure of this project is:

Reproducible Build Verificiation is a success metric:

Confirm successful generation of bit-for-bit identical binary packages across different clean build environments, demonstrating complete reproducibility.

Measurement approach: Calculate cryptographic hashes (e.g., SHA-256) of built packages and compare them against references. Hash matches indicate reproducible builds.

Wheels make the installation process quicker.

SOURCE_DATE_EPOCH is a field in the __check_build module, and it is similar to a mathematical constant, like π or e. It is crucial for version consistency in scikit-learn. Software relies on timestamps for proper functioning, just like musicians rely on precise timing.

ALGORITHMS book #

Write a reverse insertion sort algorithm #

from typing import Iterable, TypeVar, MutableSequence

def disort(data: MutableSequence) -> MutableSequence:
    """ Insertion sort elements in descending order. """
    for j in range(1, len(data)):
        k, i = data[j], j - 1
        while i >= 0 and data[i] < k:
            data[i + 1] = data[i]
            i -= 1
        data[i + 1] = k
    return data

# example usage with list
A = [31, 41, 59, 26, 41, 58]
print(disort(A))

# example usage with dictionary
d = {'a': 1, 'b': 2, 'c': 3}
print(disort(d))

# example usage with string
s = 'hello'
print(disort(s))

# example usage with tuple
t = (1, 2, 3)
print(disort(t))

# example usage with set
s = {1, 2, 3}
print(disort(s))

This algorithm results in a KeyError: 1.

attila@amp algorithms % python3 disort.py 
[59, 58, 41, 41, 31, 26]
Traceback (most recent call last):
  File "disort.py", line 19, in <module>
    print(disort(d))
  File "disort.py", line 6, in disort
    k, i = data[j], j - 1
KeyError: 1

The algorithm sorts the list, but it does not sort elements in any of the other containers. Dictionaries and sets are unordered, while strings and tuples are immutable in Python.

CS books, Python One-Liners #

>>> import numpy as np
>>> np.arange(3).reshape(3,1)
array([[0],
       [1],
       [2]])

Ice Cream Sales and Sunscreen Usage:

- Explore the relationship between ice cream sales and sunscreen usage. Do people use more sunscreen on hotter days when ice cream sales are high? A linear regression model could reveal interesting correlations.

from sklearn.linear_model import LinearRegression
# Generate random data
temperature = np.random.uniform(75, 95, 100)
ice_cream_sales = 50 + 2 * temperature + np.random.normal(0, 10, 100)

model = LinearRegression().fit(temperature.reshape(-1, 1), ice_cream_sales)

# Predictions
predictions = model.predict([[3], [4]])
print(predictions)
# [57.53417397 59.50238407]

Ker je mačka se učim slovenščina #

>>> 1 < 2 < 2
False

The second < compares 2 to 2, not the Boolean value of (1 < 2), or True < 2:

>>> 1 < 2 < 3
True