Pizza, beautiful sunny, winter day
rhythm practice #
I found an awesome rhythm/music practice, when I woke up. It is the following. Assign a rhythmic pattern to each limb, and sing 2 bars of counting 1/8-s: [1,2,3,4,5,7,8][1,2,3,4,5,6,7,8]. For example,
-
left foot 3/2 Clave
-
right foot tap on 3, 7, or vary a 1/24 triplet on the off beats 3, and 7
-
left hand, right hand plays 1/8 symmetric rhythm, for example lrrlrllr, rllrlrrl
-
sing
[do re do re do ti do ti], [do ti do ti do re do re], or different intervals, chords, harmonic changes, melody of a song
Then change the roles symmetrically between limbs. I could do this very very slowly at first, I would do it with a progressive muscle relaxation way, tensing my entire leg, or my arm and side of the chest, on a beat. The singing adds melody, intervals, and it helps understand singing as part of the rhythm. I am gaining insight into how a musical unit is made. It is like a Unix style, compact unit of music. Two bars, it is very simple, but it allows for a lot of variety, and it seems to be a very good cognitive exercise.
We can add emphasis, using a range of piano and forte, change the length of notes, and their pitch.
I am inspired by this method, I started practicing it a few months ago, sometimes trying to make rhythm when I do physical exercise. It works beautifully with juggling:
prove P(A + B) = 1 - P(A'*B') #
(A + B)' = A'B'
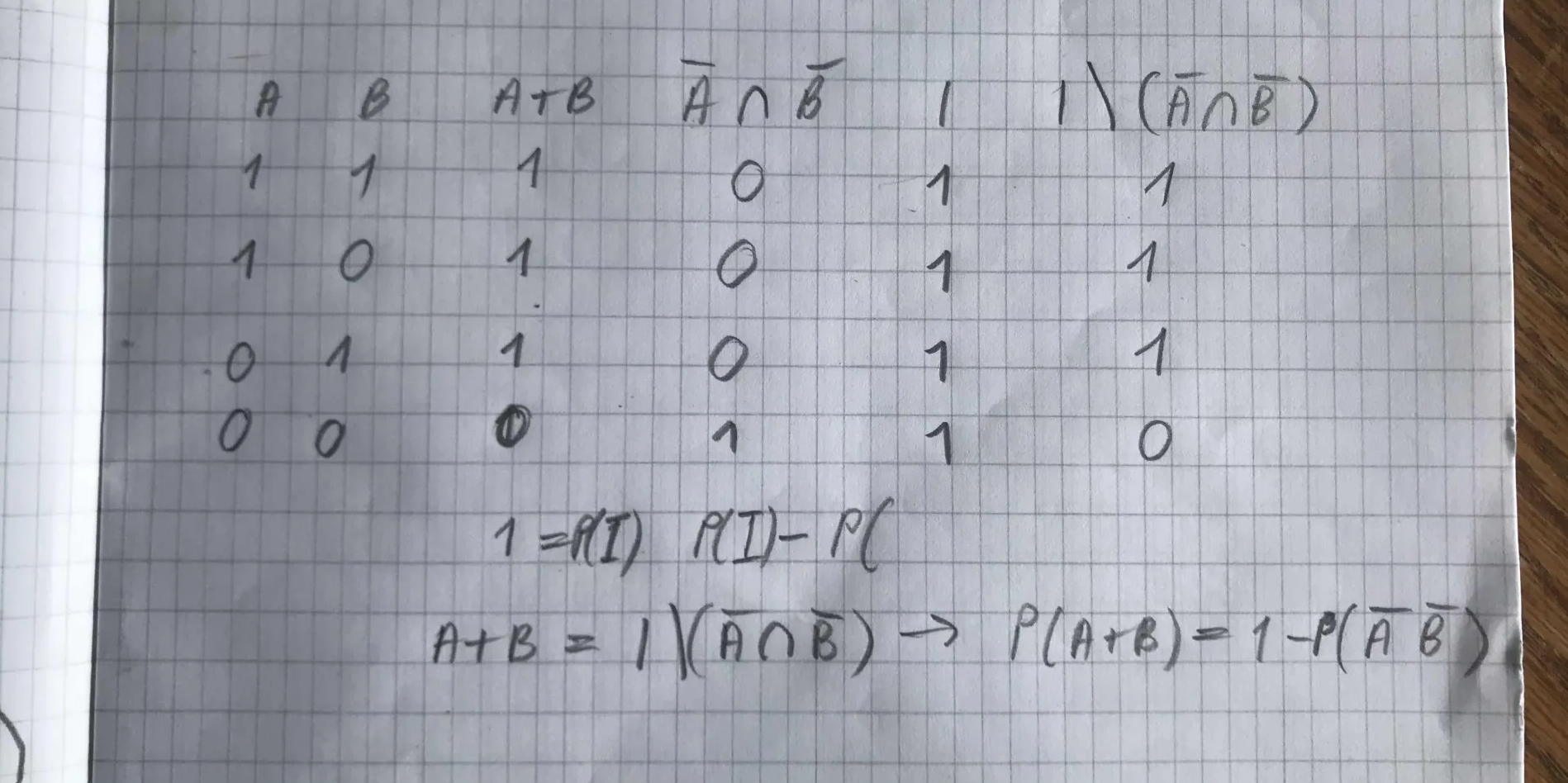
What are Q event space, and probability space for heads, when tossing three coins repeatedly?
P(A) = P(A1)+P(A2)+P(A3) = p1 + p2 + p3
Each coin has 1/2 probability for resulting in heads. If A is heads, then the likelihood of getting one heads when flipping three coins is:
P(A) = 1/2 + 1/2 + 1/2 = 3/2
My solution was wrong, because A = {1, 2, 3}, 1, 2 or 3 heads. All of the possibilities, the event space, are Q = {0, 1, 2, 3}, for tossing heads. These outcomes can result from 8 events:
TTT, TTH, THT, HTT, THH, HTH, HHT, HHH
The probability space is:
$$ p_0 = P(0) = \frac{1}{8}, p_1 = P(1) = \frac{3}{8}, p_2 = P(2) = \frac{3}{8}, p_3 = P(3) = \frac{1}{8} $$
7 of the 8 events make A true -> P(A) = 7/8
Alice, Benjamin and Chloe run a race, Alice has twice the chance of Benjamin for winning. Benjamin has twice the chance of Chloe for winning. What is the chance of Benjamin or Chloe winning the race?
P(A) = 2P(B) P(B) = 2P(C)
P((B + C)\A)
