And the thrill, should have been all
But it's only your arms, I'm out of #
I am learning jazz riffs on the guitar, I struggle with it. I also see many things from recording myself that I can improve. For example, I notice how I hold the guitar, while my fingers tensely stick together, so I practice extending my fingers, and the range of motion I use. Moving in a greater range of motion feels really amazing, and it makes it much easier to navigate the whole range of the guitar. I struggle with holding, and balancing the guitar in a comfortable posture, in which I can move and breathe freely.
Another thing I noticed is that I would move only my lips when singing, so I started to practice using my jaws, and a wider range of motion of my facial muscles, and tongue. Moving the jaws seems to alter the sound, and creates a freer passage of the air. It seems to connect the sound with the lungs. Also, I often bend/collapse my neck and spine to stare at the guitar, so now I counter this with straightening up, to feel the strings with my fingers. This creates a situation with more mistakes, which is effective in learning.
Deciphering probability formula #
I pasted all of my Python puzzles, and asked the computer agent to make puzzles of \begin{equation} P(A+B)=P(A \backslash B)+P(B)=P(A)-P(A \cdot B)+P(B), \end{equation}
To my surprise it returned a few awesome, simple puzzles, that really help me understand the meaning of these symbols, for instance:
Jungle Safari:: In a wildlife reserve, the probability of spotting either elephants (A) or zebras (B) is given by P(A+B). The probability of seeing zebras without elephants is P(A\B), and the probability of seeing elephants is P(B). Can you express P(A+B) in terms of these probabilities using the given formula?
I am now giving meaning to symbols like P(A\B), P(B). I try conjure up an image of a zebra, and think about why we have P(A\B) for seeing zebras, and P(B) for seeing elephants. P(A) is the probability of seeing zebras, but P(A\B) is the probability of seeing zebras and not seeing elephants. P(A) includes the possibility of seeing a zebra and an elephant. We might see a zebra, and an elephant as well. How likely it is to see only a zebra, with no elephant in sight?
What research questions exist of this type?
A and B are arbitrary events, A•B is A⋂B of event algebra. The likelihood of zeeing a zebra or an elephant, or both, is the sum of the likelihoods of seeing a zebra, of seeing an elephant, and of seeing the two at the same time.
P(🦓 v 🐘) = P(🦓 ) + P(🐘 ) - P(🦓 ^ 🐘 )
This is an awesome way to visualise it!
I guess one meaningful research question would be to how to apply this to playing the guitar. The ultimate low floor, high ceiling task.
I asked the computer agent to show existing open/research problems related to this equation. This equation is the inclusion-exclusion principle. Searching for these keywords results in many mathematical, and computer science papers:
Papers related to the inclusion-exclusion
I found new vocabulary in a paper, and it seems to be related to an existing, real world problem. It is a problem that relates to the inclusion-exclusion principle. I can ask the computer agent to translate abstract information into images, metaphors. Even if these mental images are not correct, I enjoy thinking about the differences, and similarities of images of abstract concepts.
Partition functions are the patterns on the coats of zebras, and elephants. It is very interesting to think in terms of wrinkles on elephants, and stripes on zebras! This seems to be an antidote to the frustration at the face of complexity.
I don't understand this formula: \begin{equation} P(n)=\sum_{k=-\infty}^{\infty}(-1)^k \cdot P\left(n-\frac{3 k^2-k}{2}\right) \end{equation}
We can search for papers related to the inclusion-exclusion principle, or P(🦓 v 🐘) = P(🦓 ) + P(🐘 ) - P(🦓 ^ 🐘 ). Then pasting entire papers to a computer agent, we can discuss it in terms of lighthearted analogies. In the context of pebbles, dry leaves, ocean waves, wrinkles on elephants, or stripes on zebras.
I think that this activity can give a sense of what real questions are out there, even if the images and formulas are not entirely accurate.
The accessibility of mathematics seems to be an open research problem in itself.
P(🦓 v 🐘) = P(🦓 ) + P(🐘 ) - P(🦓 ^ 🐘 ) #
Seeing a zebra has 2/4 probability, while seeing an elephant has 2/4. Seeing a zebra or an elephant, we add 2/4 to 2/4 and subtract the likelihood of seeing both at the same time, 1/4. 4/4 - 1/4 = 3/4.
Reading the values of the A B truth table helps in understanding the notation as well.
It feels good to be able to read something like P(A + B) in terms of something meaningful!
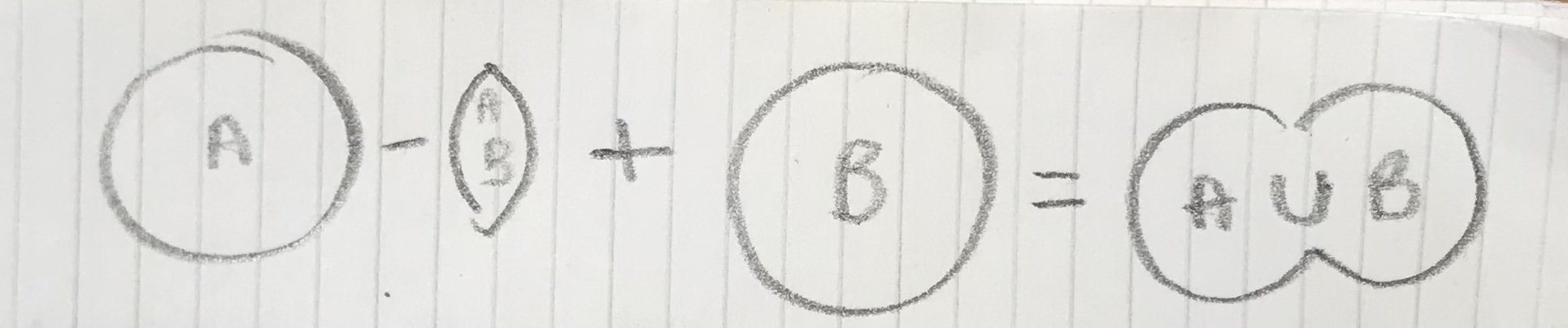
Many ways of saying the same thing. Many perspectives to a concept. Different ways of performing a song. Phrasing a harmonic progression, harmonising a melody.
This is very very cool! I am delighted at how Venn diagrams show the likelihood of wrinkles on elephants. That removing the shape of the intersection gives the probability of the union of events. Especially cool, as a short while ago I had no clue what these symbols meant, and it seemed difficult, and not accessible.
Yesterday I felt stressed about this formula, and today I can read it, and it's fun:
Consequence. If $A$, $B$ and $C$ are arbitrary events, then
$$ \begin{aligned} & P(A \cup B \cup C)= \ = & P(A)+P(B)+P(C)-P(A \cap B)-P(A \cap C)-P(B \cap C)+P(A \cap B \cap C) . \end{aligned}
Let D=B \cup C, then
\begin{aligned} A \cap D=A \cap(B \cup C)= & (A \cap B) \cup(A \cap C) \text { és } \ P(A \cap D)=P(A \cap B)+ & P(A \cap C)-P(A \cap B \cap A \cap C)= \ & =P(A \cap B)+P(A \cap C)-P(A \cap B \cap C) . \end{aligned}
\begin{aligned} & =P(A)+P(B)+P(C)-P(B \cdot C)-[P(A \cdot B)+P(A \cdot C)-P(A \cdot B \cdot C)]= \ & \quad=P(A)+P(B)+P(C)-P(B \cdot C)-P(A \cdot B)-P(A \cdot C)+P(A \cdot B \cdot C) . \end{aligned} $$
hypocycloids, R/r #
A small segment on a flanged train wheel moves backwards.
All points of a smalled circle can be put into one-to-one relationship with all points of a larger circle.
If the radii of a larger circle, and a smaller circle are R and r, and their ratio is 3, or 3/2, rolling the smaller circle inside the larger circle will produce a three vertice deltoid.
Drawing curly braces upward is so difficult! I was surprised.
What curve a square "wheel" travels when its center moves horizontally? I am reading "Wheels, life and Other Mathematical Amusements" by Martin Gardner.