Data Science Wizardry Blog by Attila Vajda

Rolling the dice

Contributing a typo fix to MathJax #

I am sieving through the contribution guidelines to find out how to make a pull request. I'm excited!

Work on real projects, and learn what is needed along the way. This is a good approach to mathematics. I wonder how to work on maths research ideas. I guess "freeform exploration" Paul Lockhart mentions, and the multidimensional, low floor high ceiling task, collaborative, "Play, visualise, investigate" approach I learn from Jo Boaler are good indicators.

def git_workflow(branch_type, version):
    if branch_type == "feature":
        return "git checkout -b {}-{} develop".format(branch_type, version)
    elif branch_type == "release" or branch_type == "hotfix":
        return "git checkout -b {}-{} develop".format(branch_type, version)
    elif branch_type == "finish":
        return "git checkout master && git merge --no-ff {} && git tag -a {} && git checkout develop && git merge --no-ff {}".format(branch, version, branch_type)

# Example usage
print(git_workflow("feature", "new_feature"))

After a few hours of research, and trying, I successfully made my first pull request!. I pasted the contribution guidelines, that I found difficult to decipher, to ChatGPT and Mixtral, and worked through the error messages until I could get the basic steps of a pull request right. We need to first make a fork, then create a new branch on the forked repo, make changes, git add . and commit as usual. Then on the GitHub website of the forked repo an option appears to make a pull request to the original repository. I am still not sure about what the develop, and master branches are.

statistics whimsy #

"I love it!"

The die roll problem

I looked at the solution, and was happy to find that C and D can indeed be given by A, and B. Furthermore, that I now understand it more clearly, as I struggled a little bit with solving the problem.

$A = \{2, 4, 6\}$: the first throw is even

$B = \{2, 4, 6\}$: the second throw is even

$C = A + B$: their product is even, at least one throw is even

$D = C' = A' + B' = (AB)'$: their product is odd, both throws are odd

Are odd * odd always odd?

I think Discovering the Arts of Mathematics books are excellent modern mathematiics primers.

Explain what even and odd numbers are. Even numbers are divisible by two without a remainder, while odd numbers result in a remainder when divided by two. 2/2 = 0, no remainder there. 1/2 = 0.5 (What is the remainder here?). Can non-integer numbers be even?

An even number is an integer that can be exactly divided by 2 without leaving a remainder. An even number is an integer of the form 2k, where k is an integer.

{2n | n ∈ ℤ}

x ≡ 0 (mod 2)

$\forall k ∈ \mathbb{Z}, x = 2k$

def is_even(x):
    return x % 2 == 0

The bitwise operator can be used in Python to check for evenness:

is_even = lambda x: x & 1 == 0

Very nice:

>>> is_even = lambda x: x & 1 == 0
>>> is_even(2)
True
>>> is_even(1)
False

probability #

n experiments, A event happens k times, (0 <= k <= n), k is the frequency of the A event.

The rate of occurrence of event A is expressed by k/n, the relative frequency of event A.

The expression for relative frequency is $g_A$.

0 <= k/n <= 1 - this is beautiful insight!

I don't understand the following, but I am getting there:

$$ k_{A_1+A_2+\ldots+An}=k_{A_1}+k_{A_2}+\ldots+k_{A_n} $$

$k$ is the frequency of an event.

$k_{A_{1}}$ is the frequency of $A_1$.

Is $k_{A_1+A_2+...+A_n}$ the frequency of the union of events?

Is $k_{A_{1}}+k_{A_{2}}+...+k_{A_{n}}$ the sum of the frequencies of all of the events?

After struggling for a while to understand the meaning of the equation, I went outside to do some exercise, and witness the sunset. Then I did a shavasana, relaxed, and the understanding of the equation emerged in my mind. The meaning of the symbols became clear. The same thing happened yesterday, while doing shavasana.

$k_{A_1+A_2+...+A_n}$ means n, if we do n experiments, we throw 10 times with a die, for instance, it's 10. It is the frequency, k, of any of the outcomes happening in n throws. $k_{A_{1}}+k_{A_{2}}+...+k_{A_{n}}$ is the sum of the frequencies of events. For example, we throw a die 10 times, we throw a 1 10 times, $k_{A_{1}} = 10$, 2 appear 0 times, $k_{A_{2}} = 0$, ... all the other numbers occur 0 times, so we have 10 + 0 + 0 + 0 + 0 + 0

expressing vectors with vectors #

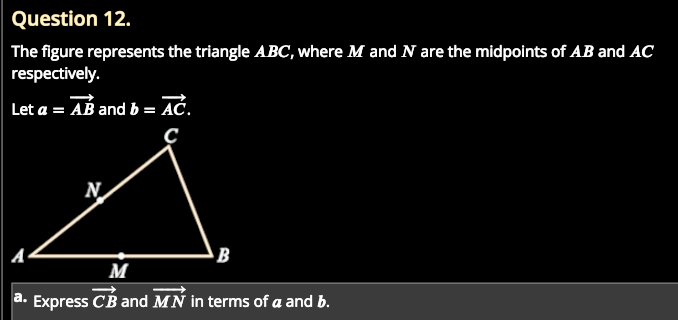
I misunderstood a task: The figure represents the triangle ABC, where M and N are the midpoints of AB and AC respectively. Let a = AB vector, and b = BC vector. Express CB and MN vectors in terms of a and b.

The figure represents the triangle ABC, where M and N are the midpoints of AB and AC respectively. Let a = AB vector, and b = BC vector. Express CB and MN vectors in terms of a and b.

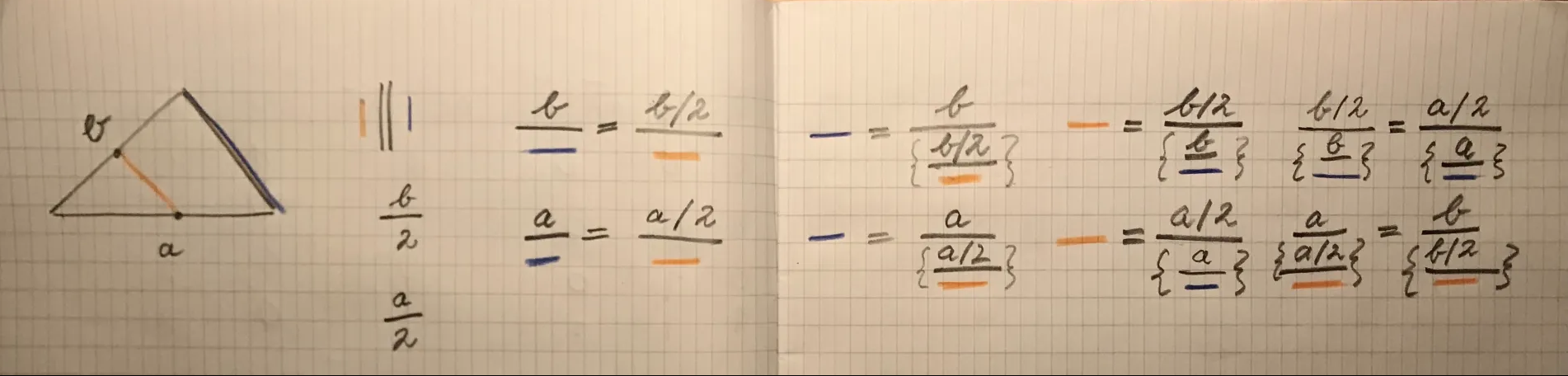
I produced the following solution, which I thoroughly enjoyed: Solving for the lengths of MN and CB, in terms of a and b.

I don't get this formula #

$$ g_{A_1+A_2+\ldots+A_n}=\frac{k_{A_1+A_2+\ldots+A_n}}{n}=\frac{k_{A_1}}{n}+\frac{k_{A_2}}{n}+\ldots+\frac{k_{A_n}}{n} $$

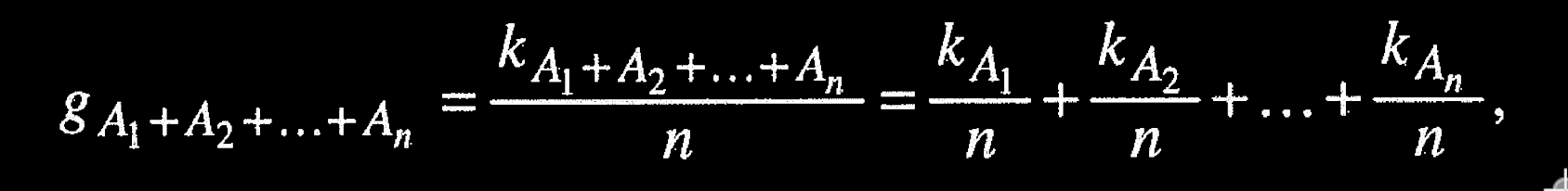The above formula Figuring out the alt text is like rubber ducking. I get to explain what the formula means. I could just use a MathJax, accessible notation!

Mathpix is a tool to convert images of maths formulas to mathematical notation formats.

Here is my attempt at expressing the formula in words, but it seems a little complicated:

Relative frequency of the union of events is equal to the ratio of the frequency of the union of events and the number of experiments. Which is also equal to the sum of the ratios of the frequencies individual events and the number of experiments.

g_A = k/n

For a die roll g_{{1}+{2}+...+{6}} = 1

g_{1, 2, 3, 4, 5, 6} = 1

The frequency of any of the events happening in n=6 experiments is k=6

g_A = k/n 6/6 = 1

Puzzling Python wind down #

t = 'abc'
d = {'sep': '-', 'end': '?'}
print(*t, **d)

This puzzle gave me trouble, so I saved it.

I th/ pt(TWR) a(t) w() -> w/d ^^^ w() app# rdm(twr) dev

Guess the output of this Python puzzle, so that good connections develop in your brain. A strength of making effort to solve this puzzle, is that good brain connectivity will develop, but frustration might result as the natural part of the learning process.

1str _ conn::brn / 1wk posb frust w/t _r 3 dif appr, alth ~kn() res?

Although I already solved this puzzle, what are three different approaches, to deepen understanding?

Approaching the puzzle from three different perspectives allows for multidimensional learning, so it will deepen understanding.