Process journal of learning by Attila Vajda

fragments of reflective proofs journal 2025 july 23

🖇 A ∧ B ⊢ B

I'm learning how to write this in Lean4!

#maybe

-- logic core
variables {A B : Prop}

Is this #perhaps saying A and B are subobjects in Ω?

Kanji: 真理 = truth

ℹ️ Each P : Prop = a predicate = subobject via χ_P

internal logic of the topos: Prop ≅ Sub(X) is Prop ≅ Sub(X) the internal logic of a topos? Ω ≅ Sub ∘ X?

play Cmaj7 ≈ space X isolate E-G ≈ subobject A

props ≅ subs

Sub(X) ≅ Hom(X,Ω)

A B : Prop ≈ subobjects A, B ↪ X

∃ₐ : Ωᵃ ⟶ Ω maps predicates f : a ⟶ Ω ∃ₐ(f) := ∨_{x∈a} f(x)

∈ ⟶ Ω^a × a

is the evaluation map

eval : Ω^a × a ⟶ Ω

(χ, x) ↦ χ(x)

(A × B) ⟶ B via projection, a special case of eval, when χ ≡ π₂

∈ : Ω^a × a ⟶ Ω -- internal to topos

∈ = apply-the-predicate!

“Does x ∈ predicate χ?” → χ(x) 🌀

∈ : Ω^{A×B} × (A×B) ⟶ Ω

∃f ∈ Hom(A×B, B). f = π₂

∃f ∈ Ω^{A×B}. f = π₂̂

"Are mappings to truth values mapped to truth values?" ∃_{A×B} : Ω^{A×B} ⟶ Ω

logic = geometry

e

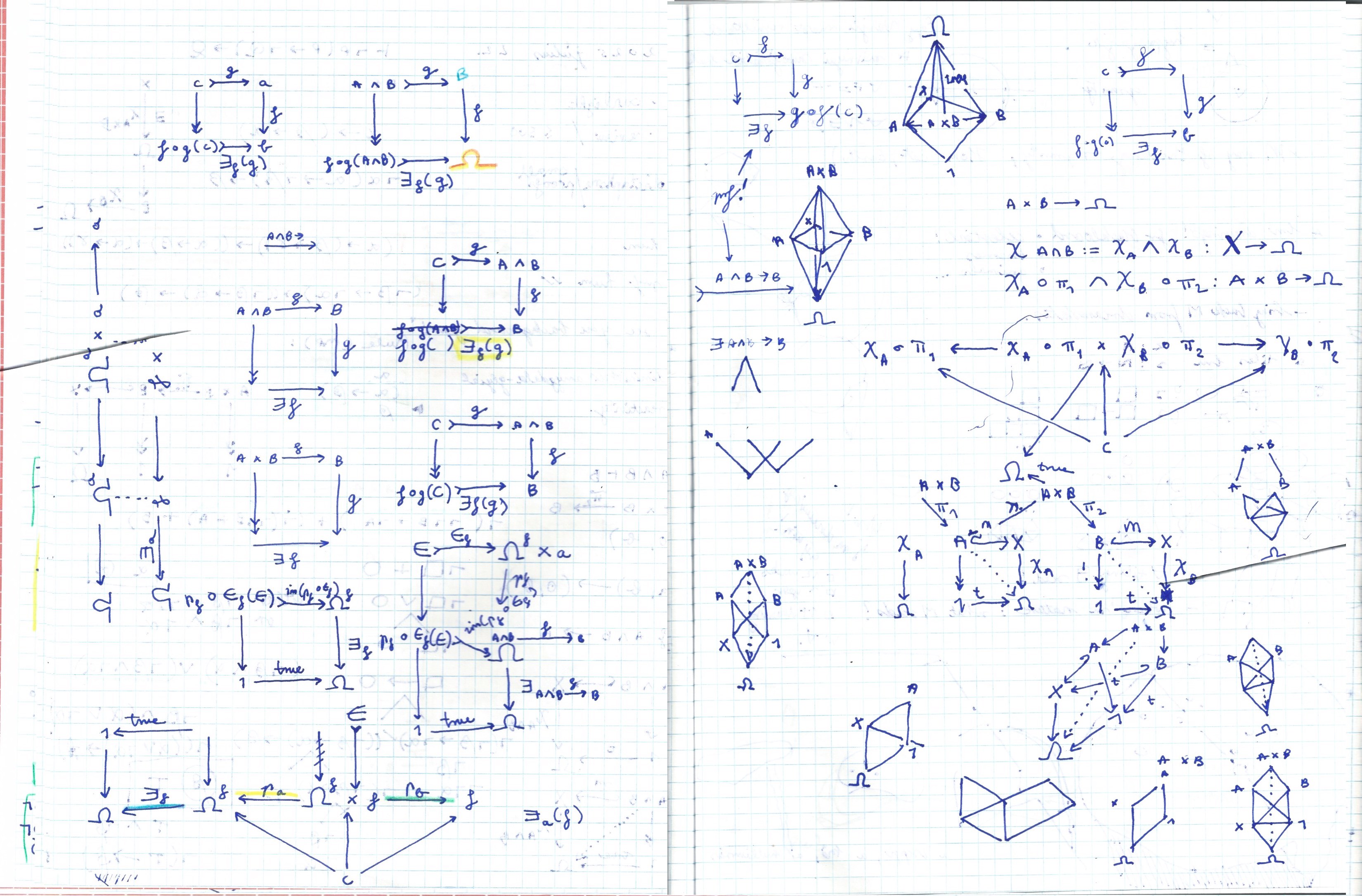
a page of journal with drawings: #

desc