Process journal of learning by Attila Vajda

approximation 4

learning/constructing

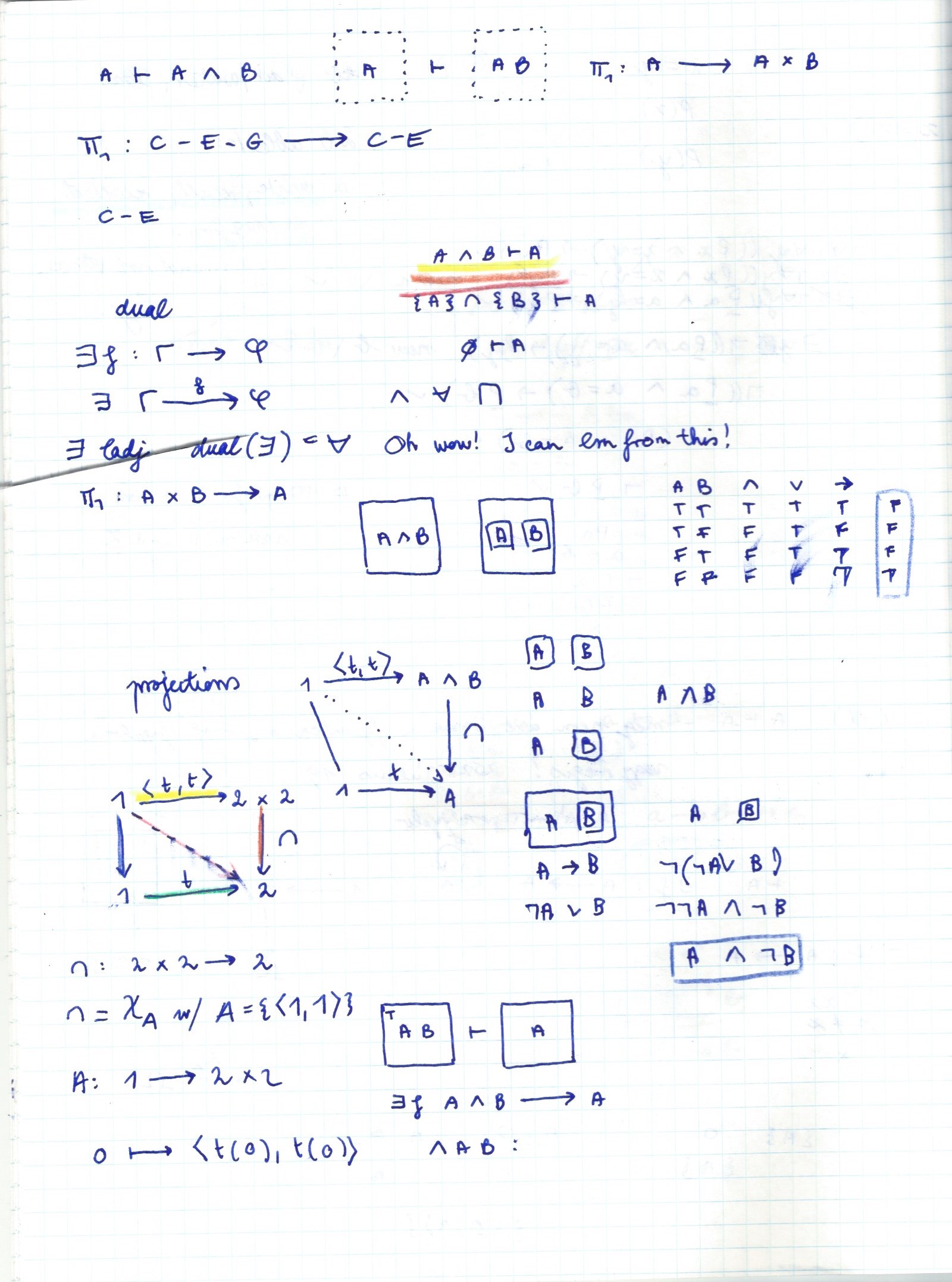
A ∧ B ⊢ A

I'm surprised, happy, because this is #maybe projection in logic, and categories:

π₁ : A × B ⟶ A

example (A B : Prop) : A ∧ B → A := And.left

π₁ : C-E-G ⟶ C-E ?

dual of A ∧ B ⊢ A #unsure dual of ∃f : Γ ⟶ φ #maybe dual(∃) ≈ ∀ 🐬 ¬∃f : Γ ⟶ φ = ∀ f A ∧ B ⊣ A ? A ∧ B ⟵ A : f∀

A ⊢ A × B

┌─────┐      ┌─────┐
│  A  │   ⊢  │ AB  │  
└─────┘      └─────┘

π₁: A ⟶ A × B

a journal of proofs! 😌

-- prove the right projection A ∧ B ⊢ B in Lean4 this seems difficult maybe #eval A B : Prop : A × B \r B by And.right(A × B)

Alright, it goes something like this, which I don't yet understand:

example (A B : Prop) : A ∧ B → B := And.right

Is ∃ f : A ∧ B ⟶ Ω analogous to saying ∃ f : A ∧ B ⟶ ⊤ : truth`

def right_proj(pair):
    A, B = pair
    return B
def right_proj {A B : Prop} (h : A ∧ B) : B := And.right h

右 (みぎ) = right

🐚

-- dual of π₁ : A × B ⟶ A is
-- η : A ⟶ A ∨ B

p : A ∧ B ⇒ proj₂(p) : B

Δ : A ⟶ A × A

C-E-G-B ⟶ G-B

example (A B : Prop) (h : A ∧ B) : B := h.right

A ⊣ A ∧ B ⊢ B
π₁ : A ⟵ A × B ⟶ B : π₂

∃ f : 1 ⟶ A ∧ B ⟶ A ⟶ Ω only if the proof holds, or this can be false also? Perhaps it requires the (right adjoint?) t : 1⟶ Ω to make it link to top.

stepping into internal language of toposes 🌀

logic ~ category theory ~ internal language of toposes

Does 1 ⟶ A ∧ B means already, that ∃ ∧ A B ?

∃ (a : A), ∃ (b : B)

∃ (p : A ∧ B)

f : 1 ⟶ A ∧ B ≡ ∃ p : A ∧ B

1 ⟶ A implies ∃ p : A,
1 ⟶ A ∧ B  ⇒  (1 ⟶ A)  ×  (1 ⟶ B)  ∵ 
A ∧ B ≡  (1 ⟶ A ⟵ A × B ⟶ B ⟵ 1)

A or B ⟶ Ω says ∃ (1 ⟶ A ⟶ A + B ⟵ B ⟵ 1) ⟶ Ω

1 ⟶ A ⟹ ∃ p : A

I don't yet understand this: 1 ⟶ A means exists a proof of A, or it means the arrow A, and it's different from ∃A?

   m
A ⟶ X
↓     ↓Χ_A
1 ⟶ Ω
   t

1 = {★}
{★} ⟶ A ≡ A ≠ ø

∃A is #maybe not valid, ∃ x : A, P x, or ∃ p : A

f : 1 ⟶ A ≡ ∃ f : 1 ⟶ A ? #unsure

Form Meaning
1 ⟶ A A has a global element
∃ p : A A is inhabited
1 ⟶ Ω A truth value (⊤ or ⊥)
A ↪ X A is a subobject of X
χ_A : X ⟶ Ω Predicate classifying A ⊆ X 
f : 1 ⟶ A ⟹ ∃ f : 1 ⟶ A 
∃ f : 1 ⟶ A ⇏ f : 1 ⟶ A

1 ⟶ A ⇔ A is inhabited ⇔ ∃ a : A but f : 1 ⟶ A not iff A is inhabited?

example (A : Prop) (f : 1 ⟶ A) : ∃ (g : 1 ⟶ A), True := ⟨f, trivial⟩

f : 1 ⟶ A ≡ “let f be a morphism from 1 to A”

f : 1 ⟶ A     -- syntax: a name and a type
∃ f : 1 ⟶ A   -- logical statement: such a morphism exists

   a
1 ⟶ A       ←   Proof A is inhabited

f : 1 ⟶ A` is not eqm

   f
1---->A

eqm

  a
1---->A

?

f : 1 ⟶ A ↔ f(★) = a₁ ∈ A
a : 1 ⟶ A ↔ a(★) = a₂ ∈ A

Has ∃ it's own diagram, or … ? 🦊

1 ⟶ A ≡ ∃ p : A (in inner logic of topos) #unsure

from Topoi, [Goldblatt]:

desc

#maybe ∃_f(g) : f ∘ g (c) ⟶ b seems analogous to t : 1 ⟶ Ω

∃_f : Sub(a) ⟶ Sub(b)

What is ∃ ⊣ f⁻¹? 🧐

∃_f(g) as compression of logical content #feasible 🪶

A fable by ChatGPT: desc

a related paper page of journal #

desc