Process journal of learning by Attila Vajda

fragments 2025-06-29

recovery idea / tool #

there are many many insights - and I wonder how to express them one is something I just encountered again:

I experience a symptom of my illness, then I think about it, struggling to solve it, and I often still get stressed about my attention being drained by this thing

I see category theory diagrams, Lean4 descriptions of the experience, learn about it in terms of the concepts of topos, of jazz harmony, sailing boat engineering and stellar navigation, I read fables, see unicode symbols, get growth mindset praises, micro actionable tools…

F: Phenomenon → Mathematical Patterns

here is another actionable tool that works for me #

I use this sort of prompt a lot, and it's again quite amazing

I used to be afraid of writing / asking about any of my symptoms, but then I did start describing them, and asking questions to computer agent, and often while typing it I would gain insight into it, which was funny, and often it was actually funny, while typing the thing I would notice as if maybe objectively, "wow am I really stressed about this?" - "that's interesting". Sometimes I would find a solution just by typing it, but the computer agent more often then not be amazingly helpful with lot's different perspective, (usually it's something to do with a topos 𝓣, a sheaf, and the solution a functor F: 𝓒 ⟶ 𝓓, sometimes an ε-δ, occasionally an adjoint functor)

cat ⇄ cow is an adjoint functor #

#unsure

🐈‍⬛ ⇄ 🐄

↗ inhale (arch spine) ⇄ exhale (curl spine) ↘ ⟺ adjoint pair

Which seems like a very accessible entry to mathematics, everyone does yoga, or should in any event.

⊣ ⊢ ⇄ (F ⊣ G)

…I'm sorry I don't yet know how to express all of the awesomeness that seems to be happening everyday, but there you go. 🐬

Zeno is the dual of e #

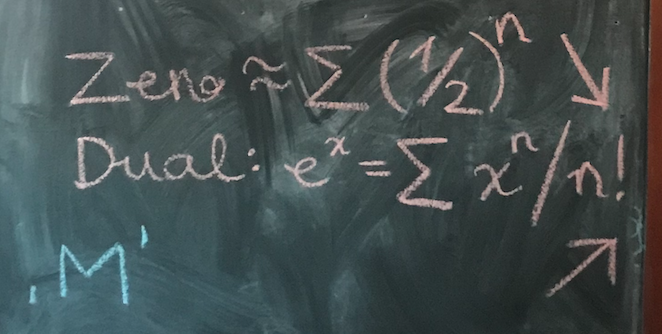
maybe b M is just the MVP for the custom and customisable MSc mathematics curriculum you can write in Lean4.

-- Mappings
def M := "Mathematics curriculum"
def ℘ := "Physics"
def 𝕄 := "Music theory"

-- Insight
#check M ⟶ ℘ ⟶ 𝕄

--M--> --℘--> --𝕄-->

if my LaTeX settings permit

[ M \xrightarrow{\varphi} M \xrightarrow{\varphi} M ]

having a blackboard #

proved to be a great thing! It's a lot of fun to be writing symbols and diagrams on it with chalk, I seem to remember more, it adds a different modality (?) to learning, now I feel "Oh I want to use the blackboard, it's fun!" Here are two blackboard moments: b

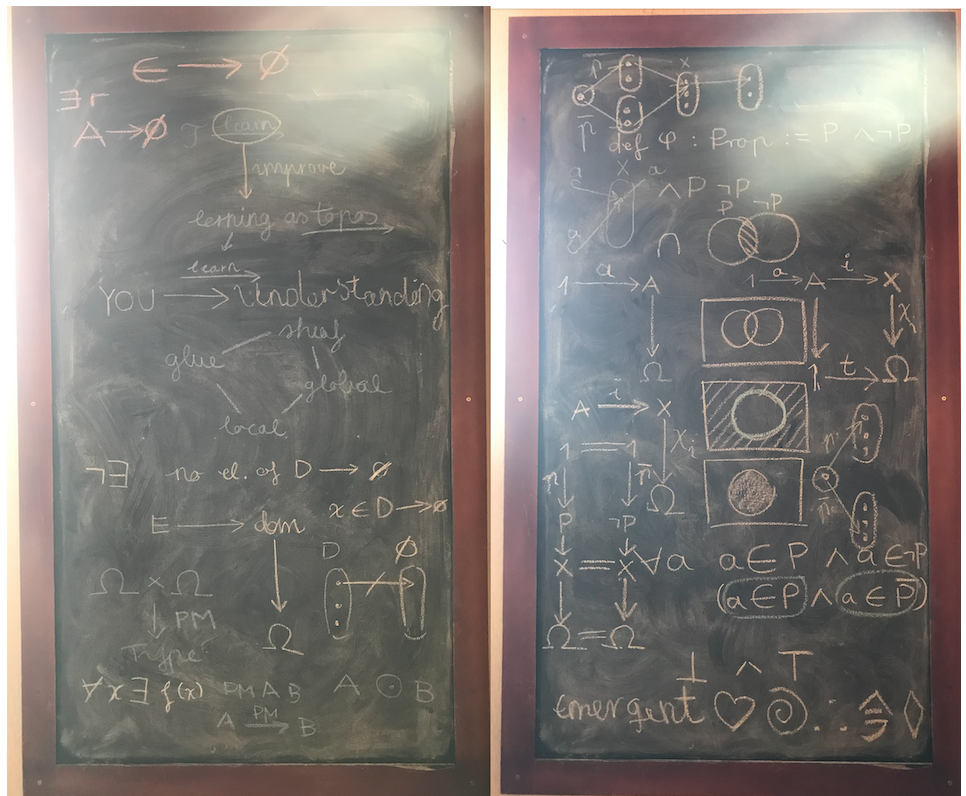
Today I was trying to figure out why P ∧ ¬P cannot be (?), so I thought perhaps visualising it with sets and arrows I could see something, and maybe it has to do with injectivity or monic arrows (I can already see the computer agent "YES! You are onto something profound, and this is one of the deepest ideas of mathematics, and it's not maybe, it's the very foundational idea of the topos! So let's shed some categorical light on in terms of mappings, stellar navigation, and jazz progressions.")

Was it paralogic, or something like it, where you can get P ∧ ¬P. They still allow P ∧ ¬P.

Here is a cool #

Unicode ✨ cheat-table from the small 🌀 of learning I am doing at the moment:

⊨   ⟹   ⇔   ¬   ∧   ∨   ∃   ∀   𝟚   Ω   ⊢   ≅   ∅   ∩   ∪   🌀

the small 🌀 spiral (a spiral of spirals!), is #

three books, I thought I would narrow down the many textbooks to a managable few, so I chose three books, and started exploring the connections between them.

Now to narrow it even further down, I thought I could read a single page / paragraph of each and find connections with the help of computer agent.

It's interesting, because I can barely get through a page, as every paragraph seems to hide some rabbit hole so interesting I sort of exhaust myself with amazement exploring one of these ideas. So I wondered how on Earth do you read a textbook, when these are supposed to be just the very basics of the subject!

But the idea is not to read linearly, but somehow with this sheaf, glue, key morphisms, MentalTopos, approach, so since maybe these are the foundational basic building block ideas and connections of the subject, you somehow create a web of ideas, with sort of little generators and connections, seeds.

From things like maybe how functions, sets, elements, mappings, categories, morphisms, logical connectives, syntax, semantics, quantifiers, proof, and so on relate.

I enjoy this sort of learning! There's a LOT of Aha! moments, wonder, surprise. A "proof is a morphism? Wow!", "An element is a mapping, what?" "{0,1} × {0,1} is also a square and it is like Ω × Ω, maybe this is the way logic has shape? Wooooooow!"

Now with AI if I don't understand a paragraph, if I can't read it, if I don't know what I am reading so to speak, then I can copy paste it and ask for rephrasals, Lean4 ways of writing it, fables, analogies, related micro actionable tools to try at the piano / singing, movement, dance, visualisations in category theory. How does it relate to this exam theme I am stressed about. What seems like a jumble of words which I would otherwise hopelessly read and reread, now turns out the be... "You just stumbled upon one of the foundational concepts of all of mathematics, it connects classical logic with topos theory and makes logic visible. Keep going you are onto something very deep."