Process journal of learning by Attila Vajda

foundations, s

I am learning the foundations #

of mathematics

the idea is to create #

minimal blog post structure

I wondered if #

it was possible (of course it is possible) how to sketch foundations so, what are the basic building blocks of foundations that we can start drawing things with

for example, if there is a combinatorics exercise, I can start drawing dots, adnd graphs, and use pebbles and so on what are the pebbles of mathematics foundations so if you sit dawn to draw basic mathematics foundations, what can you draw, or make?

can you have a necker cube, as the basic building block? "necker cube theory", or perhaps "algebraic necker cube theory"

I guess what are the underlying patterns of a foundations that are then variable?

j

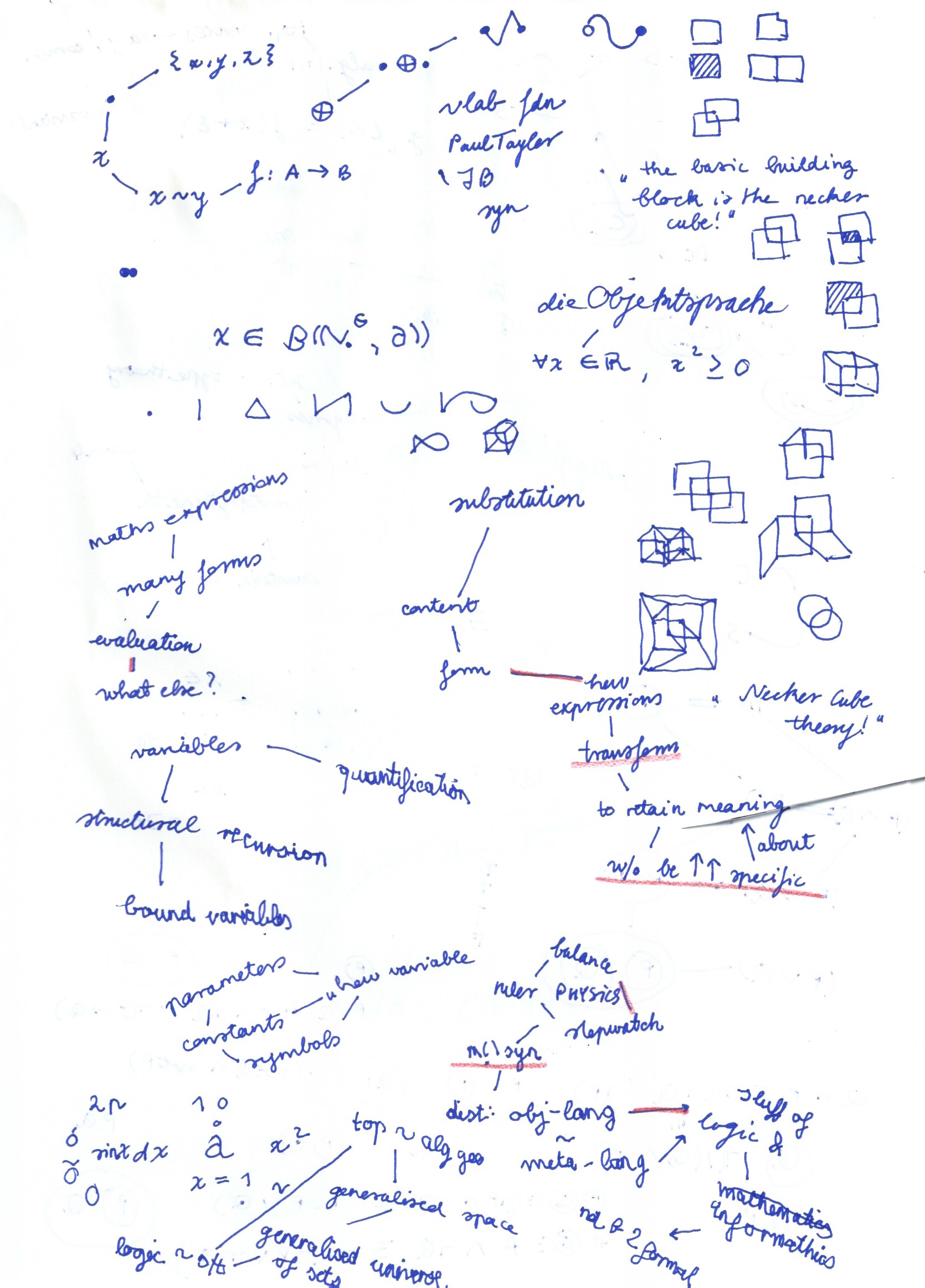
a pleasant insight #

for me was that there is the transformation of expressions to retain meaning is to do with foundations and this is perhaps why the significance of similarity of things, maybe a^2 is not exactly 🔲,

☕️ length #

I wondered how to measure time without a clock, and I realised I can have a coffee length I am working at solving this exercise for a coffee's length and then I look at the solution

I was frustrated and relieved #

when I was trying to learn what a proof was, and I noticed I get bogged down with reading and reading and reading about something,

I found searching for the word "proof" in Form and Function [Saunders MacLane] insight into what proofs were about and that they serve as explanations also, as well as a means to precision, so perhaps the "reading and reading and reading" I experienced I could now reframe as explanations.

It was nice to #

realise it was possible to perhaps look at figures and symbols, and keywords and learn

which is a dimension to multidimensional learning!

I can also rotate the book #

and the significance of things seem to shift,

so I wondered if it was possible #

and how to have basic atomic building blocks and build knowledge from those

yesterday I found I can use #

crayons for drums sticks, and create patterns on paper which seems like some sort of mapping from sound, to visual

j

a cool idea #

was that I thought now I could explain something very playful as similar to doing mathematics

like usually it is maybe said that "oh you should be doing mathematics like children play"

but now I thought "you know how mathematics is like how children play and explore the world, and are having fun? that's how you should be doing so and so"

and I thought the textbooks I see as dry and stressful, I can now reframe as products of this playful approach

maybe as someone writing "look, how cool this is!"

perhaps stress around mathematics education #

is not in harmony with this playful exploration at all

I saw a list of things that will be on a future combinatorics exam, and I immediately became stressed, then I realised hold on a minute, these are the same concepts I am usually over-excited about drawing and doodling and listening to music.

Yet there is this association of the professor is giving these examination papers and it is supposed to be very difficult, and it is a measure of your value

In fact if I fail it I can quite literally can pay the tuition fees

And the students react with "oh wow this is going to be very tough"

Yet these are like the stuff of combinatorial topology, knot theory, I'm sorry I don't yet have the vocabulary and insight, but as far as I understand these things that are served as very stressful and reserved for the talented, are like the some of the most amazing, fun, creative, things ever. That are like for everyone, and the applicability for everyday life is just unbelievable, at least in my experience.

I also noticed that there is the pattern of definition, theory proof, and I wondered what proof was, and I noticed that proof probably had some sort of meaning beyond having to learn it for exams.

What is the purpose of proof, when you are doodling around with making mathematics? In the textbook, in my experience, I noticed, it was for me like having to recite what others have found, and take an exam, and stress, and yes, why on earth would you stress about proving a theorem someone found in a mathematical world?

Prove the binomial theorem, what, why?

I sense that it is maybe more meaningful for me to reframe and see these theorems and proofs as part of that fun activity of creative exploration,

There should be no grading, and no tuition fees, this stuff should be accessible, it is not meant to be stressful, at all.

Texte brut et vivant, d’un carnet d’étudiant·e en mathématiques, où je cherche les briques premières.