Cold, sunny day, cup of coffee, morning
doing the statistics book #
Wow! I am happy that I am happy for certain things, for example, that my solution of A1'∪A2'∪A3', can be written as
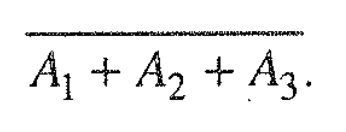
I wonder if it is appropriate to write simply ø.
$\overline{A_1+A_2+A_3}=\varnothing\implies$ the solution can be written simply as $\varnothing$. A1, A2, A3 are events, where there is water in a water pipe 1, 2, and 3. The complementer of their union means there is no water in either, an empty set.
Looking at the solution after having struggled multidimensionally, and collaboratively, is a very nice experience.
I love how maths is awesome for my thinking!
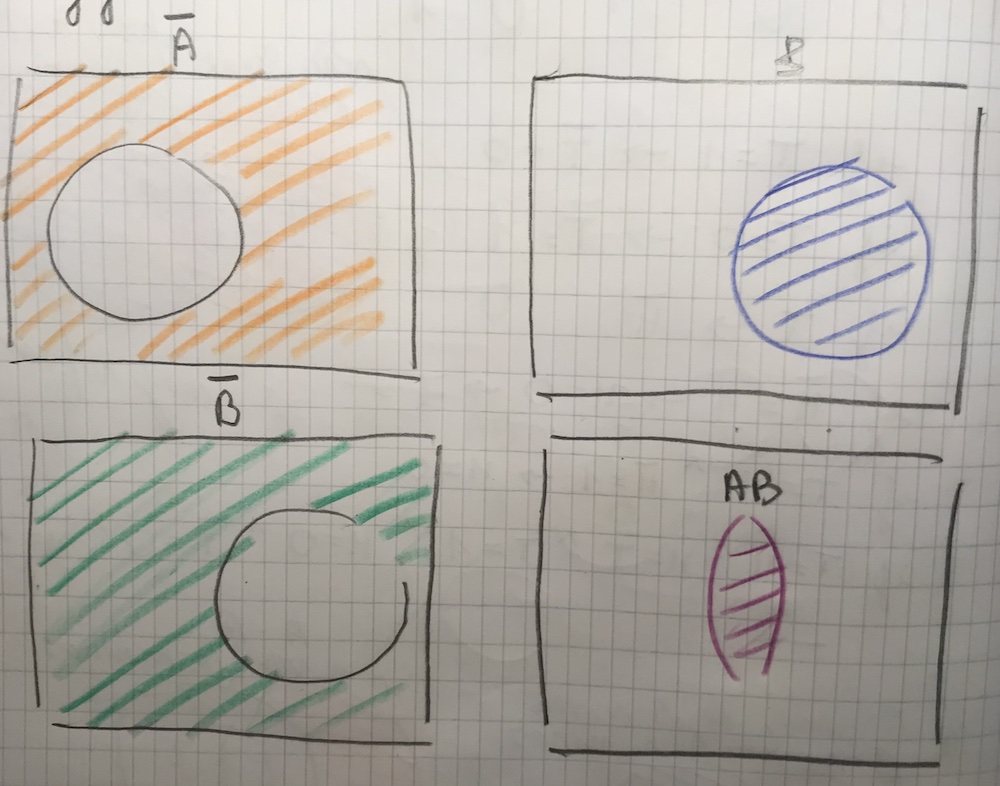
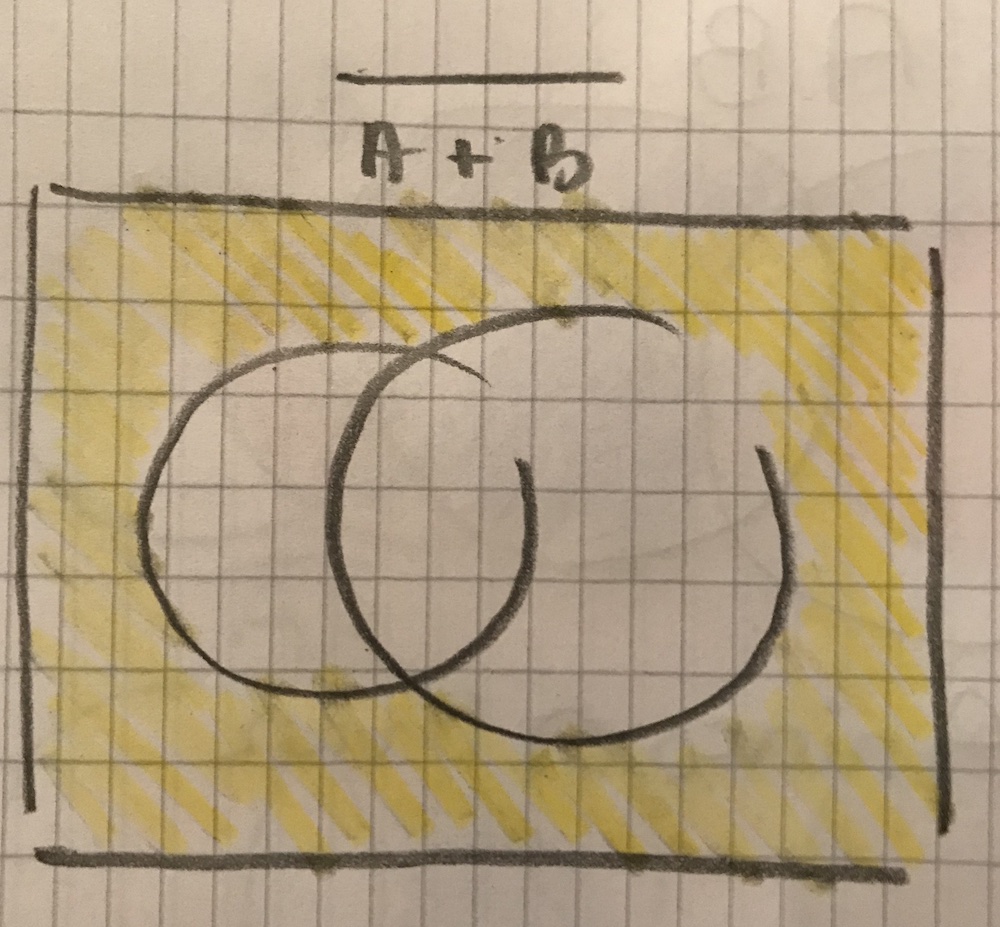
There are two conveyor belts, red, and a blue, bringing in goods to a mill. A means there are incoming products during a shift on the red threadmill, and B means there are products on the blue conveyor belt in a shift. The task is to convey in words, what the event algebra notations express.
Express in English language different given states, for example, $\overline{AB}$ and $\overline{A}B$.
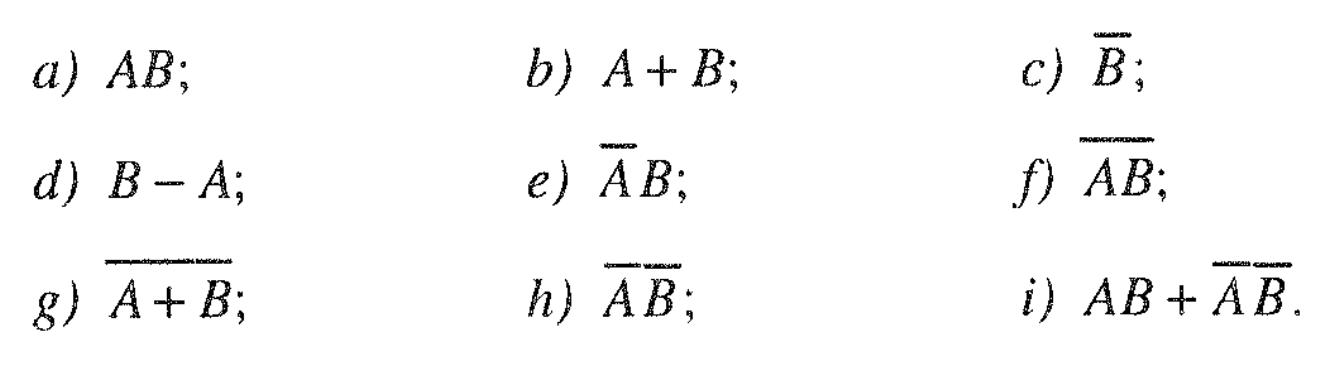
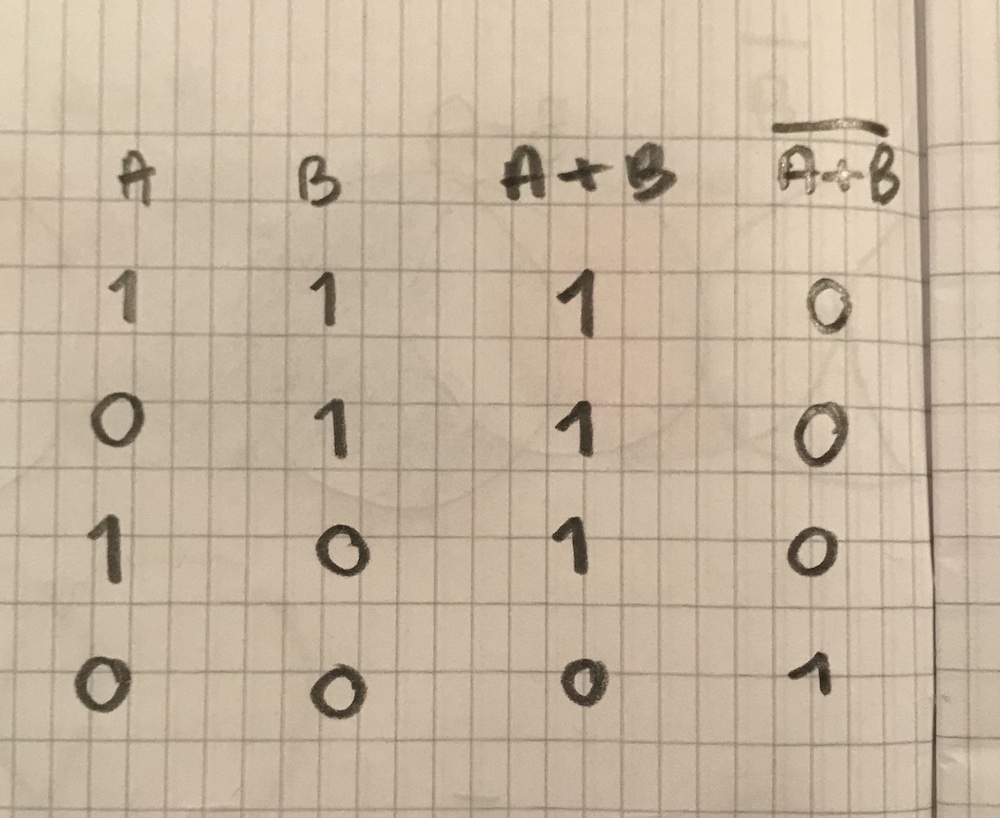
AB is A*B, or A⋂B. I made a truth table, to understand the meaning of AB.

I used the note taking technique I learned from TWR, to write create a guess in short form.
AB bth h/ gs, in other words AB means both conveyor belts have incoming goods in a shift. I was delighted to find, that the truth table values 1^1=1 is the on state, the translation of this statement, when the statement is true. Somehow, the symbols of event algebra, and formal logic, connecting with the English meaning was surprising.
$\overline{B}$ seems to mean there were no products on the blue belt, but I don't understand what $\overline{B}$ means in the truth table. Since B means an event that takes place, it is an event that has a truth value of true, of 1. It's complementer is always 0, False, when the event is not taking place.
|
|
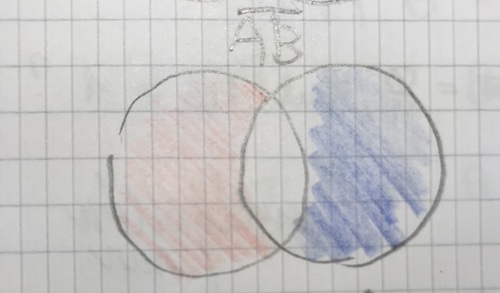
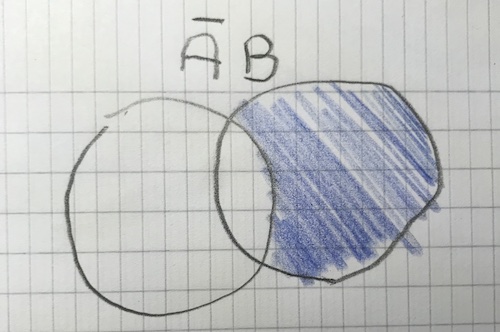
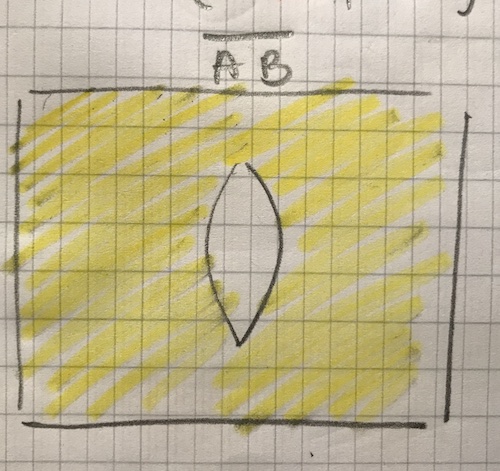
$\overline{A}B$ and $\overline{AB}$ seem tricky, because on the Venn diagram AB is the middle part, and not AB are A xor B. In terms of two events that can both happen, $\overline{AB}$ means ø.
I thought $\overline{AB}$ meant there were no products on either belts.
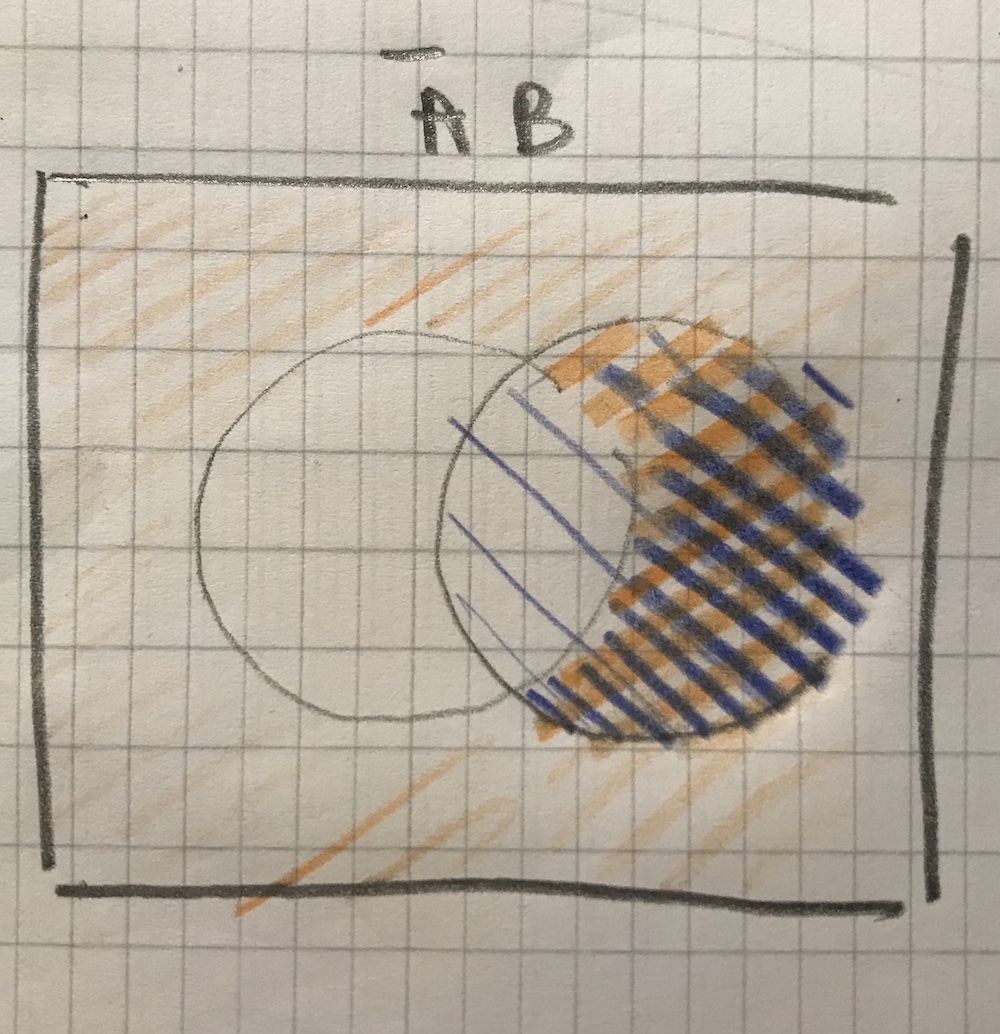
When A means the event, when there is a product on the red conveyor belt, and B means there is a product on the blue conveyor belt. I don't know, if the complement of the intersection of AB, (AB)' includes A-B and B-A, or is it the unviersal set, which is in this case ø.

Maybe because A-B ⊂ (AB)' ^ B-A ⊂ (AB)' ^ ((A-B)^(B-A)=ø) -> (AB)' = ø.
$$ Q = AB ∪ A' ∪ A-B -> A-B ⊂ (AB)' ^ B-A ⊂ (AB)' ^ ((A-B)^(B-A)) = ø, but A ⊂ (AB)' ^ B ⊂ (AB)' ^ AB ∉ (AB)' -> (AB)' = { A, B, ~(AB), $$
AB is expressed as there are products on both conveyor belts, so $\overline{AB}$ is the event, where AB is not taking place. In other words, $\overline{AB}$ is when there is a product on only one of the belts, or on non of the belts.
|
|
Mathematics is mind twisting, I like it. I thought (AB)' meant there are no products on either.
$\overline{A}$ means there is no product on red, B means, there is a product on blue. Their product, or intersection in event algebra, means that both of those statements are true. When $\overline{A}B$, there isn't a product on red, and there is a product on blue!
Haha, I don't know what is true anymore. :glassescat: These are De Morgan rules
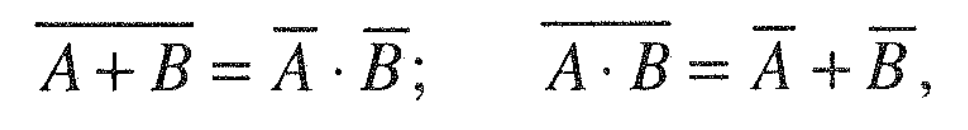
I am learning the difference between mutually exclusive events, and non-mutually exclusive events.
Mutually Exclusive Events:
- Disjoint events - Exclusive events - Incompatible events - Overlapping events (with a negative connotation) - Mutually exclusive outcomes - Excluding each other - Cannot happen at the same time - Alternative events
Non-Mutually Exclusive Events:
- Overlapping events - Non-exclusive events - Co-occurring events - Intersecting events - Non-disjoint events - Events with a common outcome - Can happen at the same time - Joint events - Complementary events (with a positive connotation)
complete probability space #
I wonder if AB, A', and A-B is the complete event space is true for event spaces with non mutually exclusive events.
From Wikipedia:
A probability space $( Ω , F , P )$ is said to be a complete probability space if for all B ∈ F with P ( B ) = 0 and all A ⊂ B one has A ∈ F. Often, the study of probability spaces is restricted to complete probability spaces.
This seems difficult to understand. I collaborate with [https://labs.perplexity.ai/](computer agents) extensively, I asked Mixtral to rephrase this statement in five ways, using but, because and so. I realised, that I already knew what $\omega$ meant, but I don't know what F means.
B in the event space F with probability zero
When tossing a coin we can never get all the time, so this event has the probability of none, because (1/2)^n approaches 0 towards infinity. Awesome. Functions, limits and graphs gain new meaning.
|
|
- Previous: Sunshine, blues day, jazz riffs and singing
- Next: AB focused meditation