Data Science Wizardry Blog by Attila Vajda

Bossa Nova, nevicato, Kako reči učenje u slovenščini?

dreams, coffee, learning slovenian and Bossa Nova #

The ChatGPT app is very good, I am now learning a little slovenian with ChatGPT. Emulating a language environment seems to be effective for language learning. My idea at the moment is to learn the basic conjugative terms but, because and so - pero, porque, entonces. Ampak, ker, tako.

Vesel sem, ker so moji video posnetki za učenje glasbe mvps dobro sprejeti. I'm glad, because my music learning video snippet mvps are well received.

I am learning Quiet Nights of Quiet Stars. The succes metrics of music learning seem to be being able to play songs, compositions, to sing. To be able to use progressions, inversions variedly and with ease.

I have been learning to sing Quiet Nights of Quiet Stars while clapping, and tapping a clave rhythm. I have been practicing Folsom Prison on the guitar, rephrasing the guitar part, and improving gestures to tell the story.

I have started reading Business Made Simple. 30 min of reading business books is excellent practice for building our freelance business.

statistics book #

baby steps. This book has two parts, probabilty theory, and the elements of statistics. I am tackling it from a zoomed out perspective, gaining and overview of the main elements.

What is the difference between an event and an event space in probability theory?

Event is the outcome of a coin toss, or die roll. Event space is the possible outcomes, such as heads, tails, or numbers 1-6. I collaborate with computer agent. I made a screen shot of the page with the main contents of the first part, and I used a Python script I wrote to convert it into text. Then I asked a computer agent for a quiz of the main topics.

*Kérlek adj egy quizt a következőkről:*
"""
VALOSZINUSEGSZAMITAS Esemény, eseménytér
Miuveletek eseményekkel A valészintiség és axiémai
Kombinatérikai dsszefoglald
Feltételes valoszintiség A teljes valoszintiség tétele Valdszintiségi valtoz6k
Diszkrét és folytonos valoszintiségi valtoz6 Varhat6 érték, szérasnégyzet és sz6rds
Egylittes- és peremeloszlisok
Eloszlas- és stiriiségfiigevény
Médusz, median, p-kvantilis Nevezetes eloszlasok Csebisev-egyenlétlenség A nagy sz4mok torvénye
"""

Event space is all the possible outcomes of an experiment. An elementary event is a distinct outcome of the experiment, dependent on uncertainty, and it cannot be the result of a combination of other events. An event is a set of elementary events.

I ❤️ statistics! It seemed like a dry subject, but now it became very intersting, and fun. A 6 element event space has 2^6 subsets, taking count of the certain, and the impossible event!

This is a visualisation of the 2^6 subsets in D3:

And another attempt, using a heatmap:

This is very cool: I solved a task from the statistics book, multidimensionally, collaborating online and with computer agents. It was to prove that AB, A' and A\B are the complete event space. Now, that I read the chapter, I am already quite familiar with the concept. If events are disjunct in Q, the intersection of any two events is ø, and the sum of all events is the certain event, then Q is a complete event space.

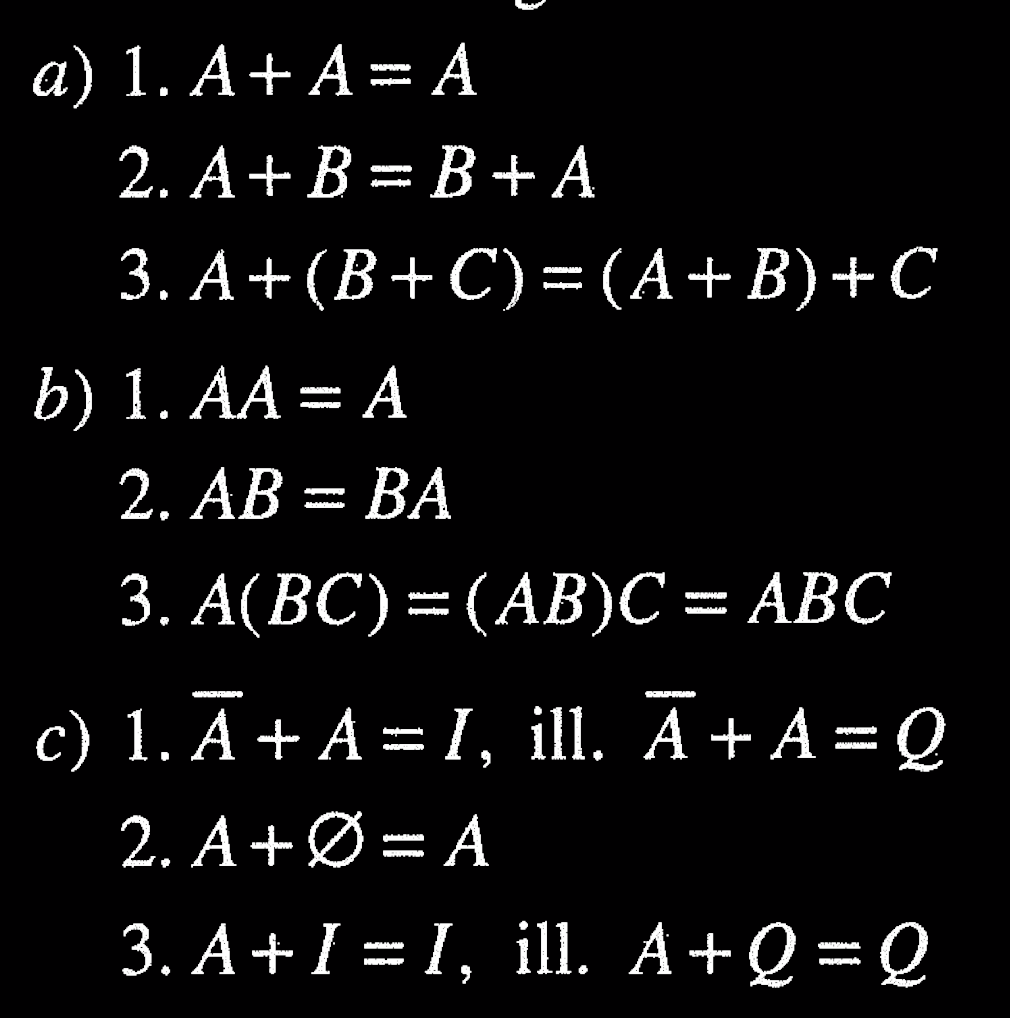
I like it. I like the reasoning aspect to mathematics. That formulas are a form of reasoning. Looking at symbols, instead of memorising, I try to focus my attention on the meaning of the writing, and it seems simple, and somehow enchanting: Axioms of event algebra

I also like concepts, like event algebra, and set algebra, and how before they seemed inaccessible concepts, now they fuse with actual things. The concepts become meaningful, and very interesting in terms of coin tosses, or die rolls. Mentally solving code puzzles started a way of thinking in me, so I enjoy staring at maths symbols, trying to figure out the "output".

Marker pen notation on glass board for event algebra

Are Boole, event, and set algebra equivalent?

Boole algebra has to do with binary values, true and false. Set algebra focuses on elements, while event algebra is concerned with probabilities of outcomes of events.

I struggle with the basic statistics tasks, working on solving them is good for me.

Event task ideas

Nice, ChatGPT got two of the same solutions. I learnt that axiom and equivalency are not the same. Axioms are assumptions, or principles accepted as true, while equivalencies are statements that express the equality of two mathematical statements.

I'm a bit confused about intersections and unions in this example. A1 ∪ A2' = 0 v 1 = 1 A1 ⋂ A2' = 0 ^ 1 = 0

What helps to see it is using curly braces: A2' = { 0 } A1 = { 1 }

{ 1 } ∪ { 0 } = { 0, 1 } { 1 } ⋂ { 0 } = ø

A1' = {A2, A3} A2' = {A1, A3} A3' = {A1, A2}

A1' ∪ A2' ∪ A3'

(A1' ∪ A2 ∪ A3) ∪ (A1 ∪ A2' ∪ A3) ∪ (A1 ∪ A2 ∪ A3')

I wonder if A1' ∪ A2' ∪ A3' is the same as (A1' ∪ A2 ∪ A3) ∪ (A1 ∪ A2' ∪ A3) ∪ (A1 ∪ A2 ∪ A3'). The second version seems to be more expressive of the fact, that two pipes are on, so it might be a more readable way to put it.

3^X+27^X=10 #

I asked the computer agent Mixtral.

3^x + (3^3)^x = 10 3^x + 3^(3x) = 10

I try to solve the simpler form x^3 = 10, because looking at simpler forms, and analogous problems can be very effective problem solving tools.

x^3 = 10 log3​(3x)=log3​(10) x⋅log3​(3)=log3​(10) x=log3​(10)

3^1 + 27^1 = 30 -> x < 1

>>> 3**(1/2) + 27**(1/2)
6.928203230275509

x > 1/2

One way to rephrase this equation is: where does the sum of the two functions equal 10? Visualisation of the composite functions in Desmos

def f(x):
   return 3**x + 27**x

a = 0.5
b = 1

while b - a > 1e-6:
   c = (a + b) / 2
   if f(c) > 10:
      b = c
   else:
      a = c

print(c)
# 0.6309289932250977

Thinking in terms of event algebra seems very intersting. I wonder if it is possible, I asked computer agent, but they couldn't solve for x. Here is another way to find it, the Newton's Method:

Here is another way to find it:
```python
from math import log

def f(x):
  return 3**x + 3**(3*x) - 10

def f_prime(x):
  return 3**x * log(3) + 9 * 3**(3*x) * log(3)

def newton(x, tol=1e-6):
  while abs(f(x)) > tol:
    x = x - f(x) / f_prime(x)
  return x

x = newton(0.5)
print(f"The solution is approximately {x}")

The graphical solution: